Compression des images hyperspectrales
These en pdf
Chapitre 5
Retour sur les critères qualité
NOUS allons maintenant évaluer l’impact du système de compression
nouvellement défini sur la qualité des images à partir des critères
sélectionnés dans le chapitre 2. Une représentation combinant les cinq critères
est d’abord exposée, son intérêt graphique est montré. Ensuite une méthode
numérique est définie pour produire une identification plus rigoureuse des
dégradations ainsi que pour démontrer l’avantage de cette méthode par
rapport à une mesure de l’erreur classique par PSNR. Enfin la méthode
est appliquée au nouvel algorithme de compression pour qualifier ses
dégradations.
5.1 Représentation des critères qualité
5.1.1 Représentation
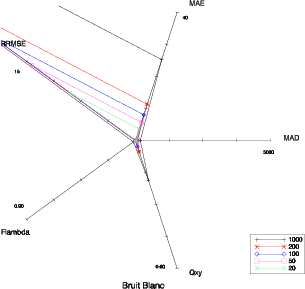
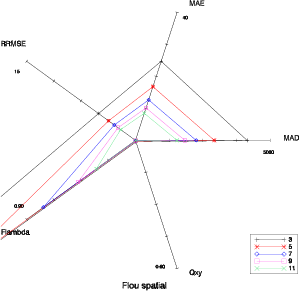
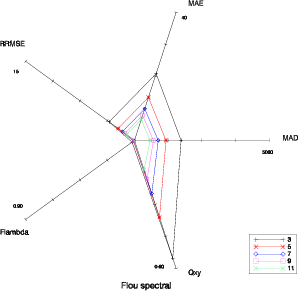
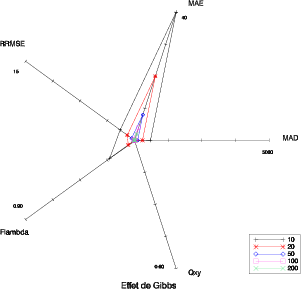
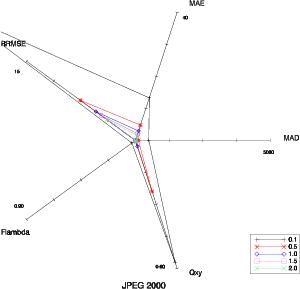
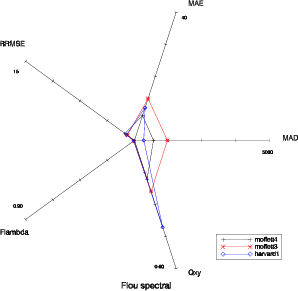
Il est délicat de trouver une représentation efficace pour visualiser la complémentarité des cinq critères sélectionnés précédemment. Un bon moyen est d’utiliser un diagramme en étoile (Fig 5.1). Les cinq axes du diagramme correspondent aux cinq critères qualité. L’échelle sur toutes les figures suivantes est la même. Pour le MAD, le MAE et le RRMSE, l’origine représente la valeur 0 (aucune dégradation). L’extrémité correspond à 5000 pour le MAD, 40 pour le MAE et 15 pour le RRMSE. Pour Fλ et Q(x,y) l’origine est la valeur 1 (aucune dégradation), le minimum étant 0.9 pour Fλ et 0.6 pour Q(x,y). La forme du diagramme est caractéristique du type de dégradation.
5.1.2 Robustesse par rapport à l’amplitude de la dégradation
Cette représentation est robuste concernant l’amplitude de la dégradation. La forme reste la même pour une dégradation donnée, il y a uniquement une différence dans le facteur d’échelle (Fig. 5.1 à 5.6). On peut également observer que les combinaisons sont possibles : le diagramme correspondant à la combinaison de flou spatial et spectral (Fig. 5.4) est logiquement la combinaison de celui du flou spatial (Fig. 5.2) et de celui du flou spectral (Fig. 5.3).
|
|
|
5.1.3 Robustesse par rapport à l’image utilisée
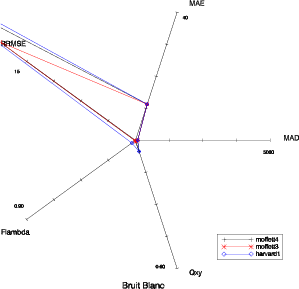
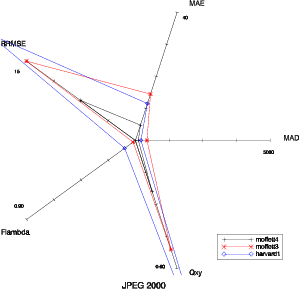
Il faut également vérifier si la représentation est robuste par rapport à l’image traitée. Cependant, certaines dégradations sont elle-même sensibles à l’image. Il est aisé de comprendre qu’un flou spatial aura une influence plus forte sur une image contenant de la ville que sur une image plutôt uniforme. La représentation est robuste pour la plupart des dégradations comme on peut le voir pour les images moffett3, moffett4 et harvard1 (Fig. 5.7 et 5.8).
|
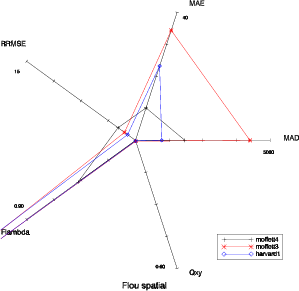
Le cas des dégradations du flou est plus complexe (Fig. 5.9 et 5.10). L’amplitude de la dégradation dépend non seulement du filtre utilisé pour effectuer le flou, mais également de l’image. Si l’image contient plus de hautes fréquences, l’impact du flou va être plus important, il est donc difficile de considérer que la dégradation a la même intensité.
|
5.2 Validation
5.2.1 Une distance entre dégradations
On voit donc que la combinaison de ces critères de qualité fournit une bonne caractérisation de la dégradation. La situation idéale à atteindre, le Graal du critère qualité, serait de pouvoir prédire précisément l’impact de la dégradation sur l’application en connaissant uniquement les 5 valeurs des critères de qualité ainsi qu’une correspondance pour une certaine image et pour certaines dégradations entre valeurs des critères de qualité et dégradations sur l’application.
Il est possible de définir un protocole de validation à différents niveaux (de difficulté croissante) pour cette combinaison de critères de qualité. On considère qu’on dispose des valeurs des cinq critères qualité pour une image avec différentes dégradations et différents niveaux pour chaque dégradation (figures 5.1 à 5.6). On dispose également de la correspondance entre chacune de ces dégradations et l’impact sur une application donnée. On peut donc essayer de prédire l’impact :
- d’une dégradation connue, mais avec un niveau différent sur cette image (1er cas) ;
- d’une dégradation inconnue sur cette image (2ème cas) ;
- d’une dégradation sur une image différente (3ème cas).
On se sert dans la suite des résultats obtenus sur l’image moffett3. Une seule image est utilisée comme référence car il est difficile d’avoir des résultats pour plusieurs applications sur une même image (c’est une des raisons qui fait l’intérêt des critères qualité). Dans le cas où une autre image est nécessaire, l’image moffett4 est utilisée.
Lorsqu’on observe une situation inconnue, on va chercher le diagramme connu
le plus proche. Pour cette notion de proximité, il nous faut définir une distance.
Une distance euclidienne classique dans un espace à 5 dimensions (les 5 critères)
est la solution la plus intuitive. Il reste cependant le problème de l’échelle entre le
différents critères : le domaine de variation du MAD qui atteint facilement des
valeurs de 2000 n’a rien à voir avec le domaine de variation de Fλ qui reste entre
0.9 et 1. Il n’y a pas de solution idéale pour ce problème, on décide donc de se
baser arbitrairement sur les échelles utilisées sur les diagrammes précédents qui
permettent de bien discriminer les différents critères à l’œil. On note par  cette
valeur normalisée.
cette
valeur normalisée.
La distance entre deux diagrammes est donc définie par :
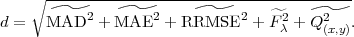 | (5.1) |
Plus cette distance est faible plus les dégradations pourront être considérées comme semblables. Nous allons maintenant vérifier si cette distance donne des résultats performants dans les trois situations illustrées ci-dessous.
5.2.2 Variation de niveau de dégradation (1er cas)
Dans le cas où un bruit blanc avec une variance de 150 est appliquée à l’image, les distances entre ce diagramme et les diagrammes de référence les plus faibles sont sans surprise les celles concernant le bruit blanc d’une variance de 200 ainsi que le bruit blanc d’une variance de 100 (Tab. 5.1). On peut donc dans ce cas correctement prédire l’impact de la dégradation sur l’application. On déduira un nombre de pixels mal classifiés entre 163 et 255, ce qui est correct : le nombre de pixels mal classifiés étant 222 (sur 65536 pixels au total).
Ce cas est également illustré pour un flou spectral d’atténuation 4 appliqué à l’image (Tab. 5.2). Les distances les plus faibles sont celles avec les flous spectraux d’atténuation 3 et 5. Cela nous donne un nombre de pixels mal classifiés entre 166 et 262, la valeur réelle étant 207.
|
5.2.3 Dégradation inconnue (2ème cas)
Pour traiter ce cas, on retire les dégradations avec JPEG 2000 de notre ensemble de situations connues, on la traite en dégradation inconnue et on regarde quelle est la situation la plus proche pour essayer de prédire le nombre de pixels mal classifiés.
Les distances obtenues sont présentées dans le tableau 5.3. La dégradation causée par JPEG 2000 est identifiée comme un mélange de bruit blanc de variance 50 et de flou spectral d’atténuation 7. Cette identification correspond à l’intuition qu’on pouvait avoir en observant les diagrammes en étoile. Les valeurs de pixels mal classifiés prédites sont de l’ordre de 112 ou 123, la valeur réelle étant 142.
|
5.2.4 Image différente (3ème cas)
Dans ce cas, on utilise les résultats obtenus sur moffett3 pour déduire les dégradations probables sur moffett4. Dans le cas d’un bruit blanc avec une variance de 100, la distance utilisée identifie correctement la dégradation comme un bruit blanc (Tab. 5.4). Cette distance interprète le bruit blanc de variance 100 sur moffett4 comme ayant le même effet qu’un bruit blanc de variance 20 sur moffett3. Le nombre de pixels mal classifiés prédit par cette méthode est de 71 alors qu’en réalité la valeur est 91.
On applique également la méthode pour une compression JPEG 2000 sur moffett4 pour un débit de 0.5 bpppb. Les distances obtenues sont présentées dans le tableau 5.5. La distance identifie bien la dégradation comme étant une compression JPEG 2000. L’image moffett4, plus uniforme, est plus facile à comprimer. Cette propriété explique que les dégradations sur moffett4 à 0.5 bpppb sont semblables à moffett3 à 1.0 bpppb. Le nombre de pixels mal classifiés estimés par cette méthode est 142, la valeur réelle étant 82. Il y a donc un manque de fiabilité dans ce cas.
|
On voit donc que dans le cas où la méthode est appliquée à une image différente, il est difficile d’évaluer précisément l’impact de la dégradation sur l’application. Toutefois la méthode permet d’identifier avec succès le type de dégradation subie par l’image. Il serait intéressant de préciser ces résultats sur un nombre d’images et d’applications beaucoup plus important.
5.2.5 Intérêt par rapport au PSNR
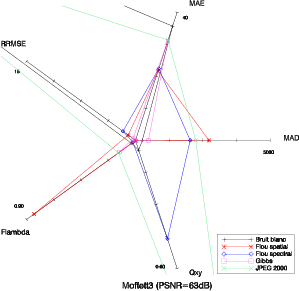
Le PSNR, ainsi que les MSE ou SNR, ne permettent pas de rendre compte de la nature de la dégradation et donc ne permet pas de prévoir l’impact sur les applications. Ce fait est illustré sur la figure 5.11. Les diagrammes sont tracés pour différentes dégradations donnant le même PSNR. Les 5 types de dégradations sont appliquées à l’image moffett3 de telle manière que le PSNR soit égal dans tous les cas à 63 dB. On voit bien sur le diagramme que bien que ces dégradations donnent le même PSNR, les caractéristiques de ces dégradations sont très différentes.
Ainsi, pour une image possédant un PSNR de 63 dB, on ne pourra pas différencier entre
- un bruit blanc de variance 2000 : 1054 pixels mal classifiés ;
- un flou spectral d’atténuation 4 : 207 pixels mal classifiés ;
- un flou spatial d’atténuation 15 : 3778 pixels mal classifiés ;
- un phénomène de Gibbs de paramètre 20 : 2029 pixels mal classifiés ;
- une compression JPEG 2000 à 0.2 bpppb : 1772 pixels mal classifiés.
Ces dégradations, qui donnent toutes un PSNR d’environ 63 dB, ont un impact sur l’application qui va varier de 207 pixels mal classifiés à 3778 pixels mal classifiés. Le PSNR échoue donc à rendre compte de l’impact d’une dégradation sur la qualité d’une image hyperspectrale pour l’utilisateur.
5.3 Impact de SPIHT-RA
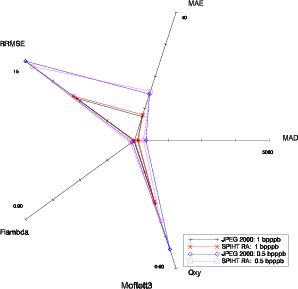
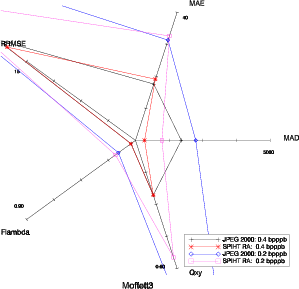
On peut réaliser une comparaison des diagrammes en étoile entre JPEG 2000 et SPIHT-RA (Fig. 5.12). La version progressive en qualité de l’algorithme (SPIHT-RA) convient mieux pour des comparaisons avec JPEG 2000 (on raisonne en terme de débit visé), c’est donc cette version qui est utilisée ici. Les diagrammes présentent de grandes similarités ce qui signifie que les deux algorithmes de compression vont causer des dégradations similaires. On voit qu’alors que JPEG 2000 est légèrement plus performant en terme de PSNR, ce n’est plus le cas pour l’ensemble des critères qualité sélectionnés. Notamment en terme de MAD (ou Emax), sur la figure 5.12 à droite, on voit que SPIHT-RA donne un MAD plus faible que JPEG 2000 à 0.2 ou 0.4 bpppb. Le calcul des distances entre JPEG 2000 et SPIHT-RA est également réalisé. Pour deux débits différents de 0.5 bpppb et 0.2 bpppb (Tab. 5.6 et 5.7), le diagramme le plus proche est à chaque fois un JPEG 2000. Il est intéressant de noter que la dégradation causée par la compression SPIHT-RA à 0.2 bpppb est plus proche de la compression JPEG 2000 à 0.3 bpppb que celle à 0.2 bpppb. SPIHT-RA semble donc plus performant à bas débit.
|
5.4 Aller plus loin
Les résultats présentés ici semblent prometteurs, tant du point de vue des performances de l’algorithme de compression défini que de la fiabilité des critères qualité. Cependant, ces résultats restent à confirmer pour une base de test plus grande : plus d’images et plus d’applications.
L’utilisation de la combinaison des cinq critères de qualité est faite ici simplement en les regroupant pour définir une distance. On a vu que cette méthode donne des résultats positifs. Il serait intéressant de raffiner cette méthode en intégrant des méthodes plus évoluées : utiliser les cinq critères comme une entrée à un réseau de neurones ayant pour sortie le nombre de pixels mal classifiés semble une chose naturelle à faire, les méthodes basées sur les Support Vector Machine (SVM) peuvent également être appliquées.