Compression des images hyperspectrales
These en pdf
Chapitre 4
Vers une plus grande flexibilité
OFFRIR plus de flexibilité à l’utilisateur d’un algorithme de
compression est probablement ce qui va diriger l’évolution des futurs
algorithmes [Pea01b]. On souhaite ainsi pouvoir décoder une image à une
résolution plus faible en accédant à un minimum de bits dans le train binaire, on
désire également accéder à une partie de l’image (en spatial ou en spectral) sans
avoir à décoder toute l’image. Ces propriétés sont obtenues tout en réduisant les
ressources (mémoire) nécessaires à la compression et à la décompression et en
posant les bases pour une compression au fil de l’eau. Cette partie de l’étude a
fait l’objet de publications [Chr06d,Chr06e].
Les propriétés de codage progressif en qualité (Fig. 4.2), en résolution (Fig. 4.3) et de résistance aux erreurs (Fig. 4.4) sont illustrées sur une image classique 2D (Fig. 4.1). Ces propriétés sont intéressantes pour des images satellites. En effet, un codage progressif en résolution est utile lors de la distribution ou de la visualisation des images : il n’est pas toujours nécessaire d’avoir l’image à pleine résolution que ce soit en spatial ou en spectral. Par exemple, la détection de nuages dans les images se fait couramment sur des images à faible résolution (quicklook). La résistance aux erreurs est particulièrement séduisante pour des applications de type sondes lointaines où le débit disponible est très faible et pour lesquelles la reprogrammation des prises de vues pose des problèmes particuliers (temps de transmission). Certains travaux sont consacrés à ces adaptations comme [Oli03,Cho05c,Xie05].
4.1 Décomposition et arbre utilisés
Selon les résultats du chapitre précédent, la structure d’arbre spatial couplée à la décomposition anisotropique donne les résultats les plus performants pour SPIHT. C’est donc cette structure qui va être utilisée dans ce chapitre (Fig. 4.5).
|
|
Rappelons que  (i,j,k) note l’ensemble des enfants du coefficient (i,j,k) du
cube hyperspectral après la décomposition présentée sur la figure 4.5. On sépare
ses enfants entre les enfant spatiaux
(i,j,k) note l’ensemble des enfants du coefficient (i,j,k) du
cube hyperspectral après la décomposition présentée sur la figure 4.5. On sépare
ses enfants entre les enfant spatiaux  spat(i,j,k) et les enfants spectraux
spat(i,j,k) et les enfants spectraux
 spec(i,j,k). On appelle ns le nombre d’échantillons (colonnes) dans la
sous-bande LLL et nl le nombre de lignes (ns et nl sont les dimensions en spatial
de la sous-bande LLL). On note nstot et nltot le nombre total de coefficients sur
une ligne ou une colonne (taille du cube hyperspectral). Ces notations sont
illustrées sur la figure 4.5. On note aussi dspat et dspec le nombre de
décompositions de la transformée en ondelettes dans les directions spatiales et
spectrale respectivement. Sur la figure 4.5, on a dspat = dspec = 3 par souci de
clarté ; en pratique, pour les résultats présentés et sauf mention contraire, on
prend dspat = dspec = 5.
spec(i,j,k). On appelle ns le nombre d’échantillons (colonnes) dans la
sous-bande LLL et nl le nombre de lignes (ns et nl sont les dimensions en spatial
de la sous-bande LLL). On note nstot et nltot le nombre total de coefficients sur
une ligne ou une colonne (taille du cube hyperspectral). Ces notations sont
illustrées sur la figure 4.5. On note aussi dspat et dspec le nombre de
décompositions de la transformée en ondelettes dans les directions spatiales et
spectrale respectivement. Sur la figure 4.5, on a dspat = dspec = 3 par souci de
clarté ; en pratique, pour les résultats présentés et sauf mention contraire, on
prend dspat = dspec = 5.
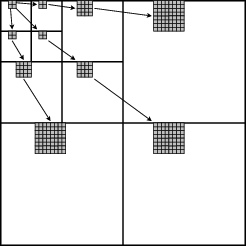
Pour la descendance spatiale, on a une relation de descendance semblable au SPIHT original, comme illustré sur la figure 4.6. À part dans les sous-bandes de plus basse fréquence et de plus haute fréquence, on a
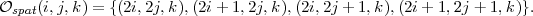 |
Les sous-bandes de plus haute fréquence n’ont pas de descendance :
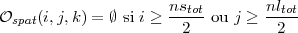 |
Et pour les plus basses fréquences (i < ns et j < nl), les coefficients sont rassemblés par groupes de 2 × 2 (en spatial) comme dans le SPIHT original (Fig. 4.6). On a alors :
- si i pair et j pair :
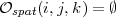
- si i impair et j pair :
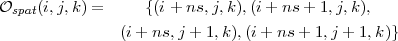
- si i pair et j impair :
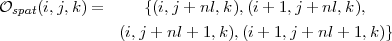
- si i impair et j impair :
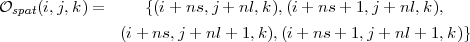
|
|
La descendance spectrale de  spec(i,j,k) est définie de manière similaire,
mais seulement pour les plus basses fréquences spatiales. On définit de manière
similaire nb comme étant le nombre de coefficients en spectral dans la sous-bande
LLL et nbtot le nombre de coefficients dans la direction spectrale pour tout le
cube.
spec(i,j,k) est définie de manière similaire,
mais seulement pour les plus basses fréquences spatiales. On définit de manière
similaire nb comme étant le nombre de coefficients en spectral dans la sous-bande
LLL et nbtot le nombre de coefficients dans la direction spectrale pour tout le
cube.
Si i ≥ ns ou j ≥ nl on a  spec(i,j,k) = ∅.
spec(i,j,k) = ∅.
Sinon, sauf pour les plus hautes et plus basses fréquences, on a
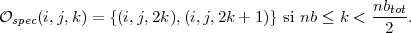 |
Pour les plus hautes fréquences, il n’y a pas de descendance :
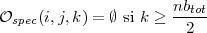 |
et pour les basses fréquences (k < nb), les coefficients sont groupés par 2 (en spectral) par analogie avec la construction de SPIHT :
- si i < ns, j < nl, k pair (et k < nb) :
 spec(i,j,k) = ∅ ;
spec(i,j,k) = ∅ ;
- si i < ns, j < nl, k impair (et k < nb) :
 spec(i,j,k) = {(i,j,k +
nb),(i,j,k + nb + 1)}.
spec(i,j,k) = {(i,j,k +
nb),(i,j,k + nb + 1)}.
Dans le cas d’un nombre impair de coefficients au niveau de la sous-bande LLL (si nb est un nombre impair), la définition précédente est légèrement modifiée et les coefficients du dernier plan spectral de la sous-bande LLL auront un seul descendant. Le regroupement des pixels dans la LLL en groupes de 2 × 2 en spatial et par 2 en spectral donne naturellement un groupe de 2 × 2 × 2 en 3D.
Avec ces définitions concernant la descendance, tous les coefficients du cube hyperspectral appartiennent à un arbre et un seul. Chacun des coefficients est le descendant d’un unique coefficient racine situé dans la sous-bande LLL (avec la structure représentée sur la figure 4.5). Il est à noter que tous les coefficients appartenant au même arbre correspondent à une zone précise de l’image originale dans les 3 dimensions.
On peut calculer le nombre maximum de descendants pour un coefficient racine (i,j,k) pour 5 niveaux de décomposition spatial et spectral (dspat = dspec = 5). Le nombre de descendants est maximum lorsque k est impair et que, au moins i ou j est impair. Dans ce cas, on a
 |
descendants spectraux et pour chacun d’eux on a
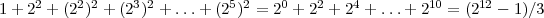 |
descendants spatiaux. On peut différencier le nombre de décompositions en spectral et en spatial, avec dspec le nombre de décompositions dans la direction spectrale et dspat dans la direction spatiale, on obtient la formule générale :
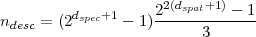 | (4.1) |
Le nombre de coefficients maximum dans un arbre est au plus 85995 (pour dspec = 5 et dspat = 5).
4.2 Le codage par groupes
4.2.1 Pourquoi ?
Pour permettre l’accès aléatoire à une portion quelconque de l’image hyperspectrale, il est nécessaire de coder séparément les différentes zones de l’image. Coder séparément les différentes portions d’une image a plusieurs avantages. D’abord, c’est une condition requise pour la compression au fil de l’eau. Ensuite, cette séparation permet d’utiliser des paramètres de compression différents en fonction de la zone de l’image, cette propriété rend possible le codage par régions d’intérêt (ROI) et le rejet (ou le codage à très basse qualité) de portions inutiles de l’image. Pour une image satellite, une partie inutile peut être une zone de nuages, pour une image médicale de type résonance magnétique, la zone inutile peut être un organe voisin de celui qui doit être observé. Un autre avantage est que les erreurs de transmission ont un impact plus limité si les zones de l’image sont codées séparement : l’erreur affecte uniquement une partie de l’image. Enfin, un des facteurs limitant de l’algorithme SPIHT est la quantité de mémoire nécessaire pour stocker les listes lors de la compression. Si le codage est fait sur des portions de l’image, le nombre maximum de coefficients en mémoire est réduit de manière très importante réduisant la mémoire requise.
Bien sûr, il y a également un désavantage à faire du codage par groupe et celui-ci sera détaillé par la suite. On souligne que seul le codage est fait par groupe, la transformée étant, elle, appliquée sur toute l’image. Il n’y a donc pas d’effet de bloc comme on peut le trouver dans le standard JPEG original.
4.2.2 Comment ?
Avec la structure d’arbre définie précédemment, des groupes apparaissent
naturellement. Un groupe 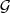 k est défini par 8 coefficients de la sous-bande LLL
formant un cube de 2 × 2 × 2 coefficients ainsi que tous leurs descendants.
Grouper les coefficients par 8 permet de tirer parti des similarités des coefficients
dans un voisinage. L’idée est similaire au codage des coefficients par groupe de
2 × 2 qui figure dans le brevet de SPIHT [Pea98] (voir Fig. 4.6) mais son
exploitation est différente. Dans le brevet de SPIHT, ce groupement permet
d’inclure un codage de Huffman car les valeurs des 4 coefficients sont fortement
liées (corrélation spatiale résiduelle). Les résultats ci-après ne prennent pas en
compte cette possibilité d’amélioration.
k est défini par 8 coefficients de la sous-bande LLL
formant un cube de 2 × 2 × 2 coefficients ainsi que tous leurs descendants.
Grouper les coefficients par 8 permet de tirer parti des similarités des coefficients
dans un voisinage. L’idée est similaire au codage des coefficients par groupe de
2 × 2 qui figure dans le brevet de SPIHT [Pea98] (voir Fig. 4.6) mais son
exploitation est différente. Dans le brevet de SPIHT, ce groupement permet
d’inclure un codage de Huffman car les valeurs des 4 coefficients sont fortement
liées (corrélation spatiale résiduelle). Les résultats ci-après ne prennent pas en
compte cette possibilité d’amélioration.
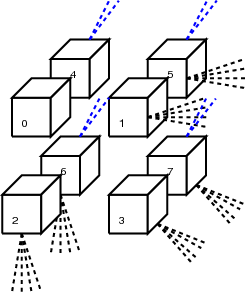
Un autre avantage de ce groupement est que le nombre de coefficients dans chaque groupe sera le même, la seule exception étant le cas où au moins une des dimensions de la sous-bande LLL est impaire. Le nombre de coefficients dans chaque groupe peut être calculé. Dans un groupe racine de 2 × 2 × 2 (Fig. 4.7), on a 3 coefficients qui ont un ensemble complet de descendants (coefficients 5, 6 et 7) dont le nombre est donné par (4.1), 3 ont seulement des descendants spatiaux (coefficients 1, 2 et 3), 1 a uniquement des descendants spectraux (coefficient 4) et le dernier n’a pas de descendant (coefficient 0). Le nombre de coefficients dans un groupe, qui est lié à la quantité de mémoire nécessaire, sera donc finalement de 262144 = 218 (pour une décomposition à 5 niveaux en spectral et en spatial).
|
|
Chacun de ces groupes 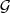 k va être codé en utilisant une version modifiée de
l’algorithme SPIHT décrit dans la partie suivante. Il faut souligner que ces
groupes n’ont rien à voir avec la notion de blocs utilisés par JPEG 2000. Ce
dernier regroupe en blocs uniquement des pixels appartenant à la même
sous-bande de la transformée en ondelettes et uniquement dans un seul plan
spectral. L’algorithme SPIHT utilisant cette séparation en groupes pour le
codage pour permettre l’accès aléatoire sera dénoté RA (Random Access) par la
suite.
k va être codé en utilisant une version modifiée de
l’algorithme SPIHT décrit dans la partie suivante. Il faut souligner que ces
groupes n’ont rien à voir avec la notion de blocs utilisés par JPEG 2000. Ce
dernier regroupe en blocs uniquement des pixels appartenant à la même
sous-bande de la transformée en ondelettes et uniquement dans un seul plan
spectral. L’algorithme SPIHT utilisant cette séparation en groupes pour le
codage pour permettre l’accès aléatoire sera dénoté RA (Random Access) par la
suite.
4.3 Permettre la progression en résolution
4.3.1 Introduction de la progression
On ne rappelle pas les détails de l’algorithme SPIHT original qui peuvent être trouvés dans la section 3.3.5. Un exemple pratique est décrit dans l’annexe B. Pour un codage progressif en résolution, on considère, ce qui est classique [Kim00,Dan03], que la sous-bande basse fréquence de la transformée en ondelettes est une version sous-échantillonnée de l’image. Pour obtenir une image à basse résolution, il suffit alors d’appliquer la transformée en ondelettes inverse (IDWT) sur les coefficients des sous-bandes de basse fréquence.
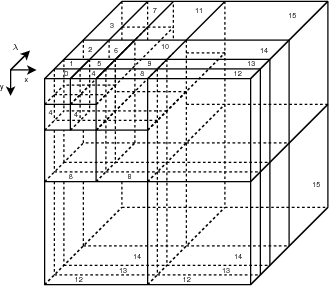
Durant le codage, SPIHT ne fait pas de distinction entre les différents niveaux de résolution. Pour pouvoir fournir différents niveaux de résolution, on doit traiter séparément chaque résolution. Pour permettre cela, on garde 3 listes pour chaque niveau de résolution Rr. Quand r = 0, seulement le plus haut niveau de la pyramide de la transformée en ondelettes sera traité (les coefficients de LLL). Pour une décomposition à 5 niveaux en spatial et en spectral, un total de 36 niveaux de résolution sera disponible comme il est illustré sur la figure 4.8 (pour des raisons de clarté sont représentés sur cette figure uniquement 3 niveaux de décomposition, soit 16 niveaux de décomposition). Chaque niveau Rr conserve 3 listes en mémoire : LSPr, LIPr et LISr.
|
|
Des difficultés apparaissent avec cette organisation. Si la priorité est donnée à un codage progressif en résolution (par rapport au codage progressif en qualité), des précautions supplémentaires doivent être prises. Les différentes possibilités pour les ordres de progression sont détaillées dans la partie suivante. On note Rrd la résolution des descendants de Rr : par exemple, la résolution descendante de R8 est R12 pour l’exemple de la figure 4.8. Dans le cas le plus compliqué, lorsque tous les plans de bits pour une résolution Rr sont traités avant la résolution des descendants rd (full resolution scalability), le dernier élément à traiter pour LSPrd, LIPrd et LISrd pour chaque plan de bit t doit être enregistré. Ce problème est illustré sur un exemple dans le paragraphe 4.3.2.
Les détails de l’algorithme sont donnés ci-dessous. On rappelle que St(i,j,k) = 0 si tous les descendants sont inférieurs à 2t, que les arbres de type A correspondent à des arbres de zéros de degré 1 (Fig. 3.17) et que les arbres de type B correspondent à des arbres de zéros de degré 2 (Fig. 3.18).
Algorithme 5. Resolution scalable 3D SPIHT (3D-SPIHT-RS)
Initialisation :
- Initialiser t au nombre de plans de bits :
- LSP0 = ∅
- LIP0 : tous les coefficients sans aucun parent (les 8 coefficients racine du groupe)
- LIS0 : tous les coefficients de la LIP0 ayant des descendants (7 sur les 8, comme un seul n’a pas de descendant).
- Pour r
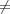 0, LSPr = LIPr = LISr = ∅
0, LSPr = LIPr = LISr = ∅
Sorting pass :
Pour chaque r variant de 0 à la résolution maximale
Pour chaque t variant du nombre de plans de bits à 0
- Pour tout (i,j,k) de LIPr qui a été ajouté à un seuil strictement supérieur au t
courant
- Écrire St(i,j,k)
- Si St(i,j,k) = 1, déplacer (i,j,k) dans LSPr à la bonne position et écrire le signe de ci,j,k
- Pour tout (i,j,k) de LISr qui a été ajouté à un plan de bits supérieur au plan de
bits courant
- Si l’entrée est de type A
- Écrire St(
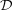 (i,j,k))
(i,j,k))
- Si St(
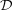 (i,j,k)) = 1 alors
(i,j,k)) = 1 alors
- Pour tout (i′,j′,k′)

 (i,j,k) : écrire St(i′,j′,k′) ; Si St(i′,j′,k′) =
1, ajouter (i′,j′,k′) à LSPrd et écrire le signe de ci′,j′,k′sinon, ajouter
(i′,j′,k′) à la fin de LIPrd.
(i,j,k) : écrire St(i′,j′,k′) ; Si St(i′,j′,k′) =
1, ajouter (i′,j′,k′) à LSPrd et écrire le signe de ci′,j′,k′sinon, ajouter
(i′,j′,k′) à la fin de LIPrd.
- Si
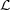 (i,j,k)
(i,j,k)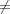 ∅, déplacer (i,j,k) à la bonne position de LISr comme
une entrée de type B
∅, déplacer (i,j,k) à la bonne position de LISr comme
une entrée de type B
- Sinon, enlever (i,j,k) de LISr
- Pour tout (i′,j′,k′)
- Écrire St(
- Si l’entrée est de type B
- Écrire St(
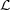 (i,j,k))
(i,j,k))
- Si St(
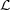 (i,j,k)) = 1
(i,j,k)) = 1
- Ajouter tous les (i′,j′,k′)

 (i,j,k) à la bonne position de LISrd
comme entrée de type A
(i,j,k) à la bonne position de LISrd
comme entrée de type A
- Enlever (i,j,k) de LISr
- Ajouter tous les (i′,j′,k′)
- Écrire St(
- Si l’entrée est de type A
Refinement pass :
- Pour tout (i,j,k) de LSPr qui a été ajouté à un seuil strictement supérieur au t courant : écrire le teme bit le plus significatif de ci,j,k.
__
Ce nouvel algorithme donne strictement la même quantité de bits que la version originale de SPIHT. Les bits sont juste organisés dans un ordre différent. Avec la structure en groupe, la mémoire nécessaire est grandement réduite. La progression en résolution, même si elle utilise plus de listes, n’augmente pas la mémoire nécessaire car les coefficients sont juste répartis entre les différentes listes.
4.3.2 Illustration sur un exemple
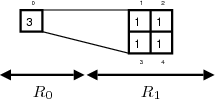
Le déroulement de l’algorithme est illustré sur un exemple simple (Fig. 4.9). Les termes de codage progressif en qualité et codage progressif en résolution seront précisés dans le paragraphe 4.3.3.
- Les coefficients 1, 2, 3 et 4 sont des descendants de 0.
- Le coefficient 0 à la résolution R0 a la valeur 3.
- Les coefficients 1, 2, 3 et 4 à la résolution R1 ont la valeur 1.
- Deux niveaux de résolution R0 et R1.
- Deux plans de bits : t = 1 avec un seuil de 2 et t = 0 avec un seuil de 1.
Regardons les différences entre le codage progressif en qualité et le codage progressif en résolution.
4.3.2.1 Codage progressif en qualité
- A la fin de R0 pour t = 1 : le seul élément significatif est le coefficient
0.
LSP0= {0} LSP1= ∅ LIP0 = ∅ LIP1 = ∅ LIS0 = {0} LIS1 = ∅ = - A la fin de R1 pour t = 1 : aucun élément significatif dans R1, pas de
changement.
LSP0= {0} LSP1= ∅ LIP0 = ∅ LIP1 = ∅ LIS0 = {0} LIS1 = ∅ = - A la fin de R0 pour t = 0 : le coefficient 0 n’est plus la racine d’un arbre de
0.
LSP0= {0} LSP1= {1,2,3,4} LIP0 = ∅ LIP1 = ∅ LIS0 = ∅ LIS1 = ∅ = - A la fin de R0 pour t = 0 : pas de changement.
LSP0= {0} LSP1= {1,2,3,4} LIP0 = ∅ LIP1 = ∅ LIS0 = ∅ LIS1 = ∅ =
On voit que dans ce cas, le parcours est très semblable au SPIHT classique et aucune précaution particulière n’est nécessaire.
4.3.2.2 Codage progressif en résolution
- A la fin de R0 pour t = 1 : le seul élément significatif est le coefficient
0.
LSP0= {0} LSP1= ∅ LIP0 = ∅ LIP1 = ∅ LIS0 = {0} LIS1 = ∅ = - A la fin de R0 pour t = 0 : le coefficient 0 n’est plus la racine d’un arbre de
0.
LSP0= {0} LSP1= {1,2,3,4} LIP0 = ∅ LIP1 = ∅ LIS0 = ∅ LIS1 = ∅ = - A la fin de R1 pour t = 1 : Le point critique est ici ! Il ne faut surtout pas
traiter les éléments de la LSP1 qui ont été ajoutés pendant le seuil
t0.
LSP0= {0} LSP1= {1,2,3,4} LIP0 = ∅ LIP1 = ∅ LIS0 = {0} LIS1 = ∅ = - A la fin de R0 pour t = 0 : pas de changement.
LSP0= {0} LSP1= {1,2,3,4} LIP0 = ∅ LIP1 = ∅ LIS0 = ∅ LIS1 = ∅ =
Pour éviter de traiter les éléments de la LSP1 ajoutés au seuil t = 0, on est obligé d’ajouter un marqueur indiquant quand traiter les éléments durant la compression. Il n’y a pas d’incidence bien sûr sur la taille du train binaire.
4.3.3 Permutation des progressions
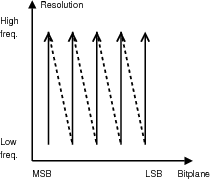
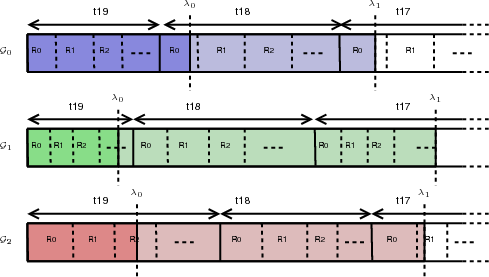
Dans la partie précédente, nous avons présenté la version la plus délicate de l’algorithme. Traiter d’abord une résolution complètement avant de passer à la suivante (Fig. 4.10 (b)) demande plus de précautions que de traiter les coefficients plan de bits par plan de bits (Fig. 4.10 (a)). Le train binaire obtenu par cet algorithme est illustré sur la figure 4.11 et nommé organisation progressive en résolution. On notera cet algorithme SPIHT-RARS (RS = Resolution Scalable), le but de cette version étant de fournir le maximum de flexibilité et notamment la séparation des résolutions spatiale et spectrales. Si la progression en résolution n’est plus une priorité et que c’est plutôt une progression en qualité qui est demandée, les boucles ’for’ de l’algorithme sur les résolutions et les plans de bits peuvent être inversées. On traitera alors complètement un plan de bits avant de passer à la résolution suivante. Dans ce cas, le train binaire est différent et illustré sur la figure 4.12. Cette organisation est nommée progressive en qualité. Cette progression en qualité donnera un train binaire très proche du SPIHT original, l’ordre de traitement au sein d’un plan de bit aura juste la contrainte supplémentaire de traiter les résolutions les unes après les autres. On notera toujours cet algorithme SPIHT-RA même si le codage et le décodage peuvent être effectués en sélectionnant la résolution pour souligner que l’objectif principal de cette version est d’obtenir la meilleurs qualité en lisant uniquement le début du train binaire. La différence du sens de parcours est illustré sur la figure 4.10.
|
|
|
L’algorithme décrit ci-dessus possède une grande flexibilité et une même image peut être codée jusqu’à un niveau arbitraire de résolution ou jusqu’à un certain plan de bits selon les deux ordres possibles des boucles. Le décodeur peut aller jusqu’au même niveau pour décoder les images. Cependant, une propriété intéressante à avoir est de pouvoir coder l’image une seule fois avec toutes les résolutions et tous les plans de bits et de choisir seulement durant l’étape de décodage les résolutions et les plans de bits à décoder. Certaines applications peuvent avoir besoin d’une image basse résolution avec une forte précision radiométrique tandis que d’autres auront besoin d’une résolution forte et se contenteront d’une radiométrie moins précise.
Lorsque l’organisation progressive en résolution est utilisée (Fig. 4.11), il est facile d’interrompre le décodage à une certaine résolution, mais si tous les plans de bits ne sont pas nécessaires, on a besoin d’un moyen pour passer au début de la résolution 1 une fois que la résolution 0 est décodée jusqu’au plan de bits souhaité. Le problème est similaire avec l’organisation progressive en qualité (Fig. 4.12) en échangeant les termes résolutions et plan de bits dans la description du problème.
Pour résoudre ce problème, on introduit un système d’en-tête de groupes qui décrit la taille de chaque portion du train binaire. La nouvelle structure est décrite sur les figures 4.13 et 4.14. Le coût de cet en-tête est négligeable : la taille de chaque portion (en bits) est codée sur 24 bits1 . Éventuellement, comme les plus faibles résolutions (respectivement les plus hauts plans de bits) ne comportent en général que quelques bits, on peut décider de les décoder complètement (coût de décodage faible) et donc de ne pas utiliser d’en-têtes pour ces faibles résolutions. Uniquement la taille de grands morceaux (au dessus de 10000 bits en général) est alors sauvegardée. Cela correspond à environ 10 valeurs de 24 bits à écrire dans le train binaire par groupe. Le coût de cet en-tête est conservé en dessous de 0.1%.
|
|
Comme dans [Dan03], on aurait pu utiliser de simples marqueurs pour identifier le début d’une nouvelle résolution ou d’un nouveau plan de bits. Les marqueurs ont l’avantage d’être plus courts qu’un en-tête codant la taille complète du groupe suivant. Cependant, les marqueurs rendent obligatoire la lecture complète du train binaire (pour trouver le marqueur), le décodeur ne peut pas se rendre directement à l’endroit désiré. Comme le coût de codage des en-têtes reste faible, cette solution est choisie.
4.4 Les désavantages du codage par groupes
Comme expliqué dans le paragraphe 4.2, le codage progressif est appliqué sur des
groupes 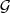 k de l’image transformée. Ces groupes ont été définis dans le
paragraphe 4.2 comme des groupements de 2 × 2 × 2 coefficients de la sous-bande
LLL ainsi que tous leurs descendants.
k de l’image transformée. Ces groupes ont été définis dans le
paragraphe 4.2 comme des groupements de 2 × 2 × 2 coefficients de la sous-bande
LLL ainsi que tous leurs descendants.
4.4.1 Conservation de la progression en qualité
Le problème de traiter les différentes parties d’une image séparément réside toujours dans l’allocation de débit pour chacune de ces parties. Un débit fixe pour chaque groupe n’est généralement pas une bonne décision car la complexité varie probablement à travers l’image. Si une progression en qualité est nécessaire pour l’image complète, il faut pouvoir mettre les bits les plus significatifs d’un groupe avant de finir le précédent. Cela peut être obtenu en coupant le train de binaire de chaque groupe pour les entrelacer. Avec cette solution, la progression en qualité ne sera plus disponible au niveau du bit à cause de l’organisation en groupes et à la séparation spatiale, mais un compromis avec des couches de qualité peut être trouvé (équivalent des quality layers), ce qui est présenté dans le paragraphe suivant. Cette organisation présente évidemment plus d’intérêt pour la version SPIHT-RA.
4.4.2 Organisation en couches et débit-distorsion
L’idée des couches de qualité est de fournir dans le même train binaire différents débits. Par exemple, un train binaire peut contenir deux niveaux de qualité : un correspondant à un débit de 1.0 bit par pixel (bpp) et un autre à 2.0 bpp. Si le décodeur a besoin d’une image à un débit de 1.0 bpp, uniquement le début du train binaire est transmis et décodé. Si une image de plus haute qualité à 2.0 bpp est nécessaire, la première couche est transmise, décodée et ensuite précisée grâce aux informations de la deuxième couche.
Comme le train binaire pour chaque groupe est progressif, on peut simplement choisir les points de coupure pour chaque groupe et chaque couche pour arriver au bon débit avec la qualité optimale pour toute l’image. On rappelle une fois encore que l’optimisation doit être globale et non locale car la qualité varie entre les groupes. Sous des contraintes spécifiques de mémoire, on peut optimiser localement.
Une méthode d’optimisation par lagrangien [Sho88] donne le point optimal de
coupure pour chaque groupe 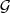 k. Comme le train binaire de chaque groupe est
progressif, choisir un point de coupure différent conduit à un débit Rk
différent et à une distorsion Dk différente. Comme les groupes sont codés
indépendamment, leurs débits sont additifs et le débit final est R = ∑
Rk. La
mesure de distorsion doit être choisie comme additive pour avoir la distorsion
finale D = ∑
Dk. Une bonne mesure est l’erreur quadratique. Soit c un coefficient
de la DWT originale de l’image et
k. Comme le train binaire de chaque groupe est
progressif, choisir un point de coupure différent conduit à un débit Rk
différent et à une distorsion Dk différente. Comme les groupes sont codés
indépendamment, leurs débits sont additifs et le débit final est R = ∑
Rk. La
mesure de distorsion doit être choisie comme additive pour avoir la distorsion
finale D = ∑
Dk. Une bonne mesure est l’erreur quadratique. Soit c un coefficient
de la DWT originale de l’image et 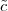 le coefficient correspondant dans la
reconstruction, alors
le coefficient correspondant dans la
reconstruction, alors
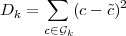 | (4.2) |
L’optimisation par lagrangien [Sho88] nous dit qu’étant donné un
paramètre λ, le point de coupure optimal pour chaque groupe 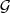 k est celui qui
minimise la fonction de coût J(λ) = Dk + λRk. Ces points de coupures sont
illustrés sur la figure 4.15. Pour chaque λ et chaque groupe
k est celui qui
minimise la fonction de coût J(λ) = Dk + λRk. Ces points de coupures sont
illustrés sur la figure 4.15. Pour chaque λ et chaque groupe 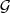 k, cette
optimisation nous donne un point de fonctionnement optimal (Rkλ,Dkλ).
Le débit total pour un λ donné est Rλ = ∑
Rkλ et la distorsion totale
Dλ = ∑
Dkλ. En faisant varier le paramètre λ, un débit visé arbitraire peut être
atteint.
k, cette
optimisation nous donne un point de fonctionnement optimal (Rkλ,Dkλ).
Le débit total pour un λ donné est Rλ = ∑
Rkλ et la distorsion totale
Dλ = ∑
Dkλ. En faisant varier le paramètre λ, un débit visé arbitraire peut être
atteint.
Cette optimisation conduit à entrelacer les trains binaires pour les différents groupes. Après le codage de chaque groupe, on a besoin de conserver les données en mémoire pour pouvoir faire cette optimisation. Il peut paraître coûteux de devoir garder les données codées en mémoire, mais il doit être souligné que pour obtenir un train binaire progressif en qualité, il est nécessaire de conserver soit l’image complète, soit l’image complète codée en mémoire. Garder l’image codée est plus économique que de garder l’image d’origine. Cette contrainte n’est pas compatible avec un codage au fil de l’eau, dans ce cas, on sera obligé de réaliser une optimisation locale en traitant des groupes de lignes et d’utiliser un buffer pour lisser les différences entre ces groupes.
|
|
|
4.4.3 Connaître la distorsion pendant la compression
Dans la partie précédente, la connaissance de la distorsion pour chaque point de coupure pour chaque groupe était implicite. Comme le train binaire pour un groupe est en général de quelques millions de bits, il n’est pas concevable de garder l’information de distorsion pour chaque point de coupure en mémoire. Seulement quelques centaines de points de coupure potentiels sont mémorisés avec le débit et la distorsion correspondant.
Connaître le débit pour un point de coupure est la partie facile : il suffit de compter le nombre de bits précédant ce point. La distorsion demande plus de calcul. Cette distorsion n’est pas recalculée complètement pour chaque point, mais mise à jour durant la compression (distorsion tracking). On considère le moment où le compresseur va ajouter un bit de précision pour le coefficient c dans le plan de bit t. Soit ct la nouvelle approximation de c apportée par ce nouveau bit. Soit ct+1 l’approximation précédente (au plan de bits t + 1).
SPIHT utilise un quantificateur à zone morte donc si le bit de précision est 0 on a ct = ct+1 - 2t-1 et si ce bit est 1 on a ct = ct+1 + 2t-1. En notant Dapres la distorsion totale après que le bit ait été ajouté et Davant la distorsion avant, on a :
Comme ce calcul peut être fait en utilisant uniquement des décalages et des additions, le coût calculatoire reste faible. D’autre part, l’algorithme n’a pas besoin de connaître la distorsion initiale comme on aurait pu s’y attendre. La méthode d’optimisation débit-distorsion reste valable si on remplace le terme distorsion par réduction de distorsion dans ce qui précède. Cette valeur de distorsion peut être très élevée et doit être conservée en interne sur un entier de 64 bits. Comme on l’a vu précédemment, on a 218 coefficients dans un groupe, pour certains d’eux (dans la sous-bande LLL), leur valeur peut atteindre 220 (avec le gain de la DWT). Les entiers sur 32 bits étant trop court, 64 bits semble un choix raisonnable et reste largement valable pour le pire des cas.
L’évaluation de la distorsion est faite dans le domaine transformé, directement sur les coefficients d’ondelettes. Cette évaluation est valide uniquement si la transformée est orthogonale. L’ondelette 9/7 de [Ant92] est quasi-orthogonale donc l’erreur réalisée par l’évaluation de la distorsion dans le domaine transformé reste suffisamment faible.
4.4.4 La formation du train binaire final
En général, on cherche à spécifier un débit R pour un niveau de qualité plutôt que de donner un paramètre λ qui n’a pas de sens pratique. Pour obtenir un débit visé, il faut trouver la bonne valeur de λ qui nous permettra d’obtenir le débit total visé R(λ) = R.
Proposition 3 ( [Sho88]). Soit λ1 et λ2 deux paramètres de Lagrange tels que λ1 < λ2. Soit (R1,D1) la solution au problème min{D+λ1R} et (R2,D2) la solution de min{D + λ2R}. Alors, on a R1 ≥ R2.
Preuve: (R1,D1) est la solution de min{D + λ1R} donc D1 + λ1R1 ≤ D2 + λ1R2. On a de même D2 + λ2R2 ≤ D1 + λ2R1. En ajoutant ces inégalités, on obtient
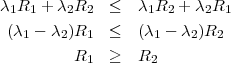









 (a)
(a) (b)
(b)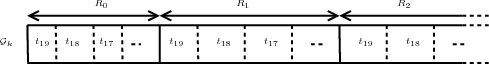
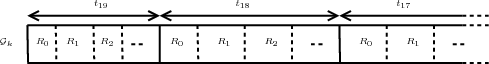
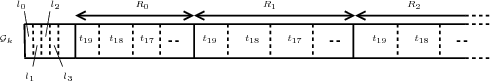
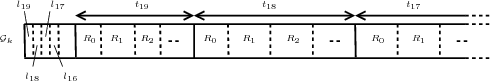

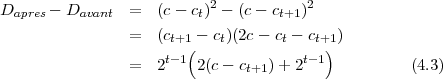
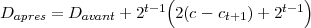
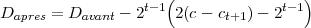
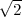 dans
les basses fréquences. Par exemple, lorsqu’on reconstitue l’image en abandonnant
les plus hautes résolutions en spatial et en spectral, il faut compenser le gain de
la DWT selon les trois directions en divisant les coefficients par
dans
les basses fréquences. Par exemple, lorsqu’on reconstitue l’image en abandonnant
les plus hautes résolutions en spatial et en spectral, il faut compenser le gain de
la DWT selon les trois directions en divisant les coefficients par 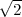 pour obtenir
une radiance correcte.
pour obtenir
une radiance correcte.
 (a)
(a) (b)
(b) (c)
(c)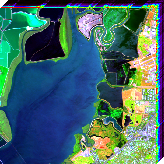 (d)
(d)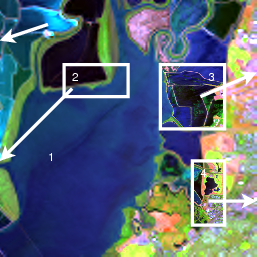 (a)
(a)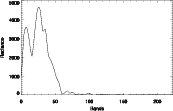 (b) spectre de 1
(b) spectre de 1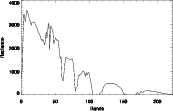 (c) spectre de 2
(c) spectre de 2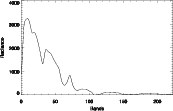 (d) spectre de 3
(d) spectre de 3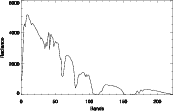 (e) spectre de 4
(e) spectre de 4