Compression des images hyperspectrales
These en pdf
Chapitre 3
Compression des images hyperspectrales
REVENONS maintenant sur la compression avec ce chapitre qui présente
l’adaptation des méthodes de transformée en ondelettes pour les propriétés
spécifiques de l’hyperspectral. Une première partie développe les possibilités du
standard de compression JPEG 2000. La seconde partie s’attache à trouver la
transformation en ondelettes optimale pour les images hyperspectrales. Enfin,
une adaptation des structures d’arbres de zéros est faite pour appliquer les
algorithmes EZW et SPIHT aux images hyperspectrales. Cette partie de l’étude
a fait l’objet de publications [Chr06a,Chr06b,Chr06c,Chr07a,Chr07b].
3.1 JPEG 2000 pour l’hyperspectral
3.1.1 La norme JPEG 2000
JPEG 2000 est la norme la plus récente pour la compression d’image fixe. Une
documentation complète est disponible sur le sujet, on peut voir par
exemple [Tau02,Sko01]. Cette partie propose uniquement une présentation des
points clés de la norme.
Cette norme a été définie pour fournir un cadre à une grande variété
d’applications compressant les images avec différentes caractéristiques (images
naturelles, images scientifiques multicomposantes, texte codé sur deux niveaux…)
pour différentes utilisations (transmission en temps réel, archive, ressources
limitées…).
Les principales fonctionnalités de JPEG 2000 sont, entre autres, le tuilage
d’images de grande taille, le codage de régions d’intérêt (region of interest ou
ROI) tout en proposant le codage d’images de dynamiques variées avec différents
nombres de composantes. La partie 1 du standard [ISO02] comprend la plupart
des fonctionnalités de JPEG 2000 pouvant être utilisées sans payer de royalties
ou de frais de licence. La partie 2 contient les extensions [ISO04]. La plupart des
implémentations actuelles de JPEG 2000 correspondent uniquement la partie
1.
Le codeur JPEG 2000 est basé sur le modèle de codage par transformée.
Pour coder une image à une composante, une transformation multirésolution en
ondelettes est d’abord appliquée. L’annexe A concerne les principaux
aspects de l’utilisation de la transformée en ondelettes. Dans le cas d’une
compression sans pertes, c’est l’ondelette Le Gall 5/3 qui est utilisée, sinon c’est
l’ondelette de Daubechies 9/7. Pour la compression sans pertes, c’est une
transformation d’entiers en entiers basée sur une implémentation en lifting
scheme de la transformée en ondelettes [Dau98]. Ces transformations ont été
choisies pour leur capacité à effectuer une décorrélation efficace d’une
image.
La partie codage entropique de JPEG 2000 est assez complexe pour
respecter la flexibilité demandée par la norme. Pour permettre le codage
progressif ainsi que la résistance aux erreurs de transmission, le codage
est basé sur un codage par blocs avec points de troncatures optimaux
(Embedded Block Coding with Optimal Truncation ou EBCOT) [Tau00].
EBCOT est la raison principale des excellentes performances en terme de
débit-distorsion de cette norme. Chaque sous-bande issue de la transformée en
ondelettes est partagée en blocs de taille relativement faible (64 × 64
pixels en général). Chacun de ces blocs est ensuite codé indépendamment
pour produire un train binaire progressif. Une quantification scalaire est
utilisée pour la partie 1 de la norme tandis que la quantification vectorielle
est disponible dans les extensions. Le codage entropique est réalisé par
un codeur arithmétique contextuel. Les symboles sont codés à partir
de modèles de probabilités pour 18 contextes différents. La norme ne
spécifie pas d’allocation de débit et donc sur ce point, l’utilisateur est libre
de faire ce qu’il veut. Néanmoins, une méthode populaire et largement
utilisée est l’algorithme PCRD-opt (Post Compression Rate Distortion
optimization) qui détermine le point optimal de troncature pour chacun des
blocs [Tau00].
Pour les images multicomposantes à trois bandes (une image couleur classique
par exemple), une transformation standard entre les couleurs est appliquée avant
le codage par JPEG 2000. Cette transformation convertit l’espace naturel RGB
(Red Green Blue) dans un espace moins corrélé YCrCb (une luminance et deux
chrominances). Ensuite, le codeur JPEG 2000 classique est appliqué à
chaque composante. L’algorithme d’allocation de débit (PCRD-opt) est
ensuite utilisé de manière globale pour répartir le débit entre toutes les
composantes.
3.1.2 Adaptation aux images hyperspectrales
Les parties 1 et 2 de la norme JPEG 2000 sont destinées au codage des images
fixes en niveau de gris ou des images avec 3 bandes de couleurs et éventuellement
un quatrième canal alpha (pour spécifier la transparence). Dans ces parties,
aucune transformation intercomposante n’est définie à l’exception de la
transformation couleur. Cependant, la partie 2 prévoit l’utilisation de
transformations intercomposantes pouvant être précisées par l’utilisateur, avec,
entre autres, la transformation en ondelettes. La partie 10, également connue
sous le terme de JP3D, vise plutôt les images tridimensionnelles aussi
isotropiques que possible [wg104]. Ces spécifications ne conviennent pas aux
images hyperspectrales qui ne sont pas isotropiques et ont, par exemple, une
corrélation bien plus forte dans la direction spectrale que dans les directions
spatiales. Par conséquent, la partie JP3D du standard ne convient pas à la
compression des images hyperspectrales. Nous proposons donc plutôt
d’utiliser les extensions de la norme (partie 2) en introduisant l’utilisation
de transformées intercomposantes avant d’appliquer le codage JPEG
2000.
L’implémentation de référence de JPEG 2000 est le Verification Model (VM).
Le VM est utilisé par le comité JPEG 2000 pour les expérimentations et
évoluera au final en implémentation de la norme JPEG 2000 [wg101]. Pour cette
étude, la version VM 9.1, la plus récente, est utilisée pour évaluer les
performances de compression de la norme JPEG 2000 adaptée aux images
hyperspectrales. Une correction est nécessaire pour pouvoir décomprimer les
trains binaires obtenus en utilisant la transformée intercomposante, cette
correction est détaillée dans l’annexe C. Une autre implémentation récente et
populaire de JPEG 2000, Kakadu, version 5.0 est également utilisée pour
confirmer les résultats. Le détail des lignes de commande et des options utilisées
est donné dans l’annexe C.
Comme il a été précisé, les parties 1 et 2 de la norme ne donnent pas de
spécifications pour les cas où l’image possède plus de 3 bandes (transformation
couleur). Cependant, le VM permet à l’utilisateur de fournir une matrice de
transformation permettant une transformée en cosinus discrète (DCT) ou
une transformée de Karhunen-Loeve (KLT). Cela est fait en utilisant
l’option -Mlin du VM. Une autre option (-Mtdt) permet d’appliquer une
transformée en ondelettes (DWT 9/7) entre les différentes composantes.
Dans ces deux cas, la transformation 1D est appliquée sur la dimension
spectrale avant d’utiliser l’encodage classique JPEG2000 sur les images
résultantes. Une optimisation débit-distorsion par lagrangien est une option
utile car les composantes ont des propriétés statistiques différentes après
la compaction d’énergie réalisée par la transformation (option -Flra).
Sans cette option, le VM a du mal à atteindre le débit visé sur certaines
images.
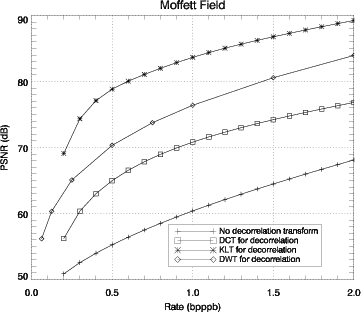
La figure 3.1 compare les performances de plusieurs transformations
intercomposantes : DCT, KLT et DWT en terme de PSNR (Eq. 2.11) en fonction
du nombre de bits par pixel par bande (bpppb).
Introduire une décorrélation intercomposante des données avant le codage
JPEG 2000 permet d’augmenter de manière importante les performances. La
KLT donne les meilleurs résultats car elle est adaptée aux données et est
optimale en terme de décorrélation et de concentration d’énergie. La DWT
augmente significativement les résultats tandis que la DCT présente des
performances plus faibles.
La KLT est spécifique à chaque image et les matrices de transformation
doivent donc être recalculées en fonction des données. Ce calcul est coûteux en
terme de complexité : il est nécessaire de calculer la matrice de covariance ainsi
que les vecteurs propres. Cette complexité est dissuasive pour la plupart des
applications particulièrement lorsque le nombre de bandes augmente.
Dans le cas des images multispectrales une approche utilisant une KLT
générique, calculée sur plusieurs images est envisagée [Thi06]. Dans ce cas,
il n’est plus nécessaire d’effectuer la diagonalisation de la matrice de
covariance, il suffit d’effectuer la transformation. Avec 224 bandes, l’opération
reste encore impossible en implémentation matérielle comme le montre le
tableau 3.1. L’approche par transformation en ondelettes paraît plus
adaptée, surtout dans le cas hyperspectral où le nombre de composantes est
important.
|
| | # bandes | Surface (mm2) |
|
| | 16 | 6 |
| 64 | 99 |
| 128 | 400 |
| 256 | 1500 |
|
| | |
| Tab. 3.1: | Surface de silicium nécessaire pour l’implémentation matérielle
(ASIC) de la transformée KLT (sans le calcul de la matrice de
transformation) en fonction du nombre de bandes spectrales. La limite
actuelle est de l’ordre de 110mm2 [Alc06]. |
|
L’algorithme JPEG 2000 nécessite des ressources importantes (principalement
pour le codeur arithmétique et l’allocation de débit) ce qui n’est pas possible
particulièrement dans le contexte d’une implémentation spatiale où les contraintes
sont très fortes. A notre connaissance, il n’existe qu’une seule implémentation de
JPEG 2000 adaptée aux contraintes spatiales [VB05]. L’auteur de cette
implémentation indique que les performances sont significativement moins
bonnes que Kakadu dans le cas de la compression avec pertes à cause de
l’impossibilité d’implémenter l’optimisation débit-distorsion. Le Consultative
Committee for Space Data Systems (CCSDS), un groupe de travail regroupant
les principales agences spatiales mondiales (NASA, JAXA, ESA, CNES) a émis
des recommandations pour les systèmes de compression bord [Yeh05]. La
recommandation consiste à regrouper les coefficients de la transformée en
ondelettes dans une structure similaire à celle des arbres de zéros plutôt que
d’utiliser la norme JPEG 2000. Le but de cette implémentation est d’alléger
la complexité vis-à-vis de la norme JPEG 2000. Les performances de
JPEG 2000 dans notre étude sont à voir plutôt comme une référence à
atteindre, le but étant ici d’obtenir des performances proches de cette
référence tout en gardant une complexité faible. La version de JPEG 2000 au
fil de l’eau (scan-based mode), plus réaliste pour une implémentation
spatiale donne elle-même des performances réduites par rapport à la
référence.
La réduction de complexité par rapport à JPEG 2000 n’est pas obtenue
directement par l’utilisation de la transformation en ondelettes selon les 3
directions, mais il apparaît que les ondelettes permettent l’utilisation d’outils
performants et simples. C’est donc la transformée en ondelettes qui est choisie
pour la décomposition.
3.2 Choix de la décomposition optimale
Avant d’adapter les arbres de zéros aux images hyperspectrales, il est nécessaire
de définir une extension de la transformation en ondelettes performante pour les
images hyperspectrales. La plupart des extensions actuelles sont basées sur des
décompositions isotropiques [Tan03,Kim03], or, comme il a été montré dans les
chapitres précédents, les données hyperspectrales ne sont clairement pas
isotropiques. Dans le domaine de la compression vidéo, des structures
anisotropiques sont utilisées avec succès [He03,Cho03]. Cependant, aucune
justification théorique n’a été donnée concernant le choix de cette structure
particulière et des décompositions plus efficaces pourraient exister. De toute
façon, le meilleur choix pour les données vidéo n’est pas nécessairement le
meilleur pour les images hyperspectrales à cause des propriétés statistiques
différentes.
Le problème de la recherche de la décomposition en ondelettes optimale pour
signaux à une dimension a été exploré dans plusieurs publications (par
exemple [Coi90]). Pour les images naturelles 2D, les possibilités de décomposition
ont souvent été restreintes à des quadtrees (conduisant à des sous-bandes carrées)
mais ont évolué avec les décompositions anisotropiques [Xu03]. Plusieurs critères
ont été utilisés pour choisir la décomposition optimale : sélection basée sur
l’entropie [Coi92] ou sur un compromis débit-distorsion [Ram93] par exemple.
L’avantage principal du dernier choix est qu’il propose simultanément l’allocation
de débit entre les différentes sous-bandes [Sho88].
3.2.1 Décomposition anisotropique 3D en ondelettes
Classiquement, pour les images 2D, la transformée en ondelettes est isotropique
i.e. pour une sous-bande donnée, le niveau de décomposition dans la direction
horizontale est le même que dans la direction verticale. Cette alternance entre
décomposition des lignes et des colonnes conduit à des sous-bandes carrées
,
l’équivalent en 3D étant des cubes. C’est le cas de la décomposition
multirésolution définie par Mallat ou de la décomposition en paquets
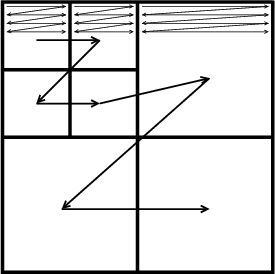
d’ondelettes pour les images [Mal89]. Un exemple de la décomposition
multirésolution classique est illustré sur la figure 3.2. Les coefficients
gris représentent des valeurs proches de zéros, tandis que les noirs et
blancs correspondent respectivement à des valeurs fortement négatives ou
positives.
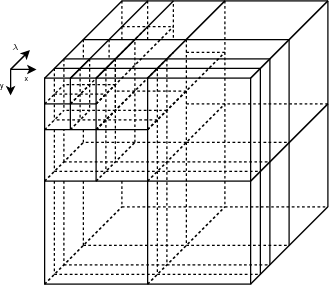
Le terme anisotropique est plus général que l’utilisation courante du terme
paquets d’ondelettes. Dans la plupart des cas, le terme paquets d’ondelettes
désigne une transformation en quadtree conduisant à des sous-bandes carrées.
Cette utilisation est justifiée par le fait que les images 2D classiques ont des
propriétés statistiques similaires dans toutes les directions. Un exemple de
décomposition anisotropique est donné sur la figure 3.3. On s’aperçoit
ainsi qu’une telle décomposition non isotropique permet d’isoler une sous
bande contenant beaucoup d’énergie (Fig. 3.3, sous-bande 1), tandis
que les autres sous-bandes contiennent une majorité de coefficients nuls
(la sous-bande 2 par exemple). Ceci permettra un codage efficace de
l’image.
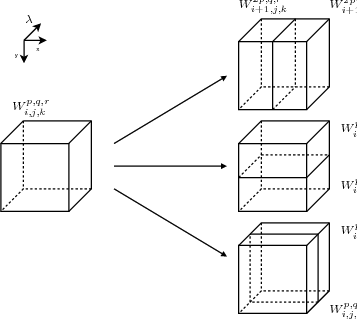
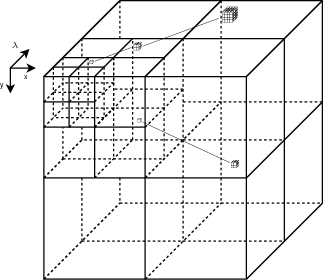
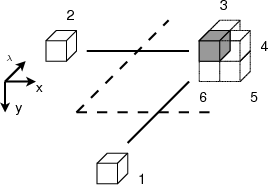
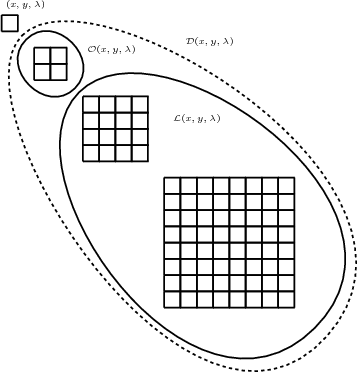
On note Wi,j,kp,q,r une sous-bande de la décomposition 3D en ondelettes
(Fig. 3.4) :
- i,j,k étant le niveau de décomposition selon, respectivement, les
lignes, les colonnes et les spectres (déterminant la taille de la
sous-bande).
- p,q,r étant respectivement l’index de ligne, de colonne et de spectre.
Cette notation est illustrée sur la décomposition multirésolution pour une
image 2D dans l’annexe A.
Une relation peut être définie au niveau des espaces vectoriels des
sous-bandes. Pour une décomposition selon les lignes, l’espace des ondelettes
anisotropiques vérifie
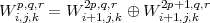 | (3.1) |
où ⊕ est la somme directe de deux espaces vectoriels.
Pour une décomposition selon les colonnes, on a
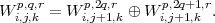 | (3.2) |
et selon les spectres
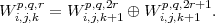 | (3.3) |
À chaque étape de la décomposition, pour toutes les sous-bandes, il est
possible de choisir la direction de la décomposition ce qui accroît la flexibilité de
l’espace des décompositions. La décomposition multirésolution et les
décompositions en paquets d’ondelettes sont toutes deux des cas particuliers de
cette représentation.
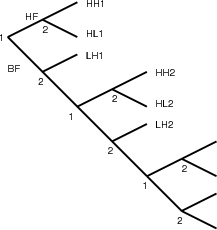
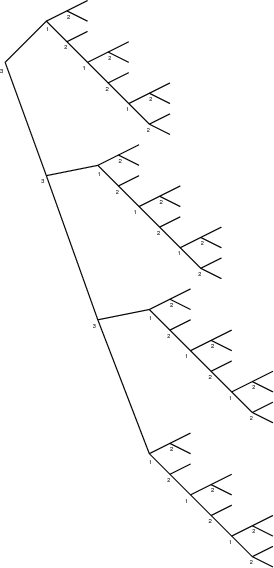
Une représentation simple et bien adaptée pour ce type de décomposition
peut être faite sous la forme d’arbre (Fig. 3.5 et 3.6). Chaque nœud porte un
numéro, indiquant le sens de la décomposition (x, y ou λ), et deux branches,
correspondant aux deux sous-bandes.
Il faut noter que la correspondance arbre-décomposition n’est pas bijective.
Deux arbres différents peuvent donner la même décomposition. Par exemple,
décomposer sur x puis sur chacune des deux sous-bandes décomposer sur y
donne la même décomposition que décomposer d’abord sur y puis sur x
pour chacune des deux sous-bandes. Les arbres correspondant à ces deux
transformations seront différents. Par contre, un arbre donne bien une seule
décomposition possible.
La représentation sous forme d’arbre se prête particulièrement bien à une
programmation récursive.
3.2.2 Optimisation débit-distorsion
3.2.2.1 Le problème d’allocation
Le problème de l’allocation de débit, i.e. la distribution du budget de
bits entre chaque sous-bande est un problème classique en compression
de données. Shoham et Gersho ont traité le problème dans le cadre de
la théorie débit-distorsion [Sho88]. Leur solution consiste à minimiser
la distorsion sous une contrainte de débit en utilisant la méthode du
lagrangien.
Dans le contexte de la décomposition en ondelettes, différentes types de
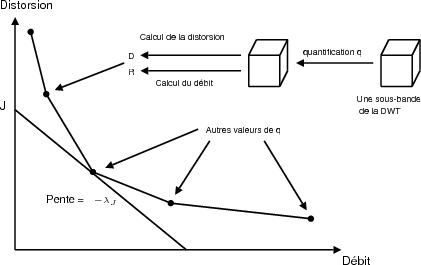
quantificateurs peuvent être utilisés pour les différentes sous-bandes. Chaque
quantificateur donnera une valeur de débit et une valeur de distortion pour
chaque sous-bande (Fig. 3.7). On appelle S l’ensemble fini des combinaisons de
quantificateurs pour les sous-bandes et B un élément de S. Un choix de B
indiquera le quantificateur utilisé pour chacune des sous-bandes de la
décomposition. Le problème est de minimiser la distorsion D(B) sous la
contrainte de débit total R(B) dans le budget total Rc :
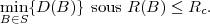 | (3.4) |
En utilisant la méthode du lagrangien, on transforme cette minimisation sous
contrainte en minimisation d’une fonction de coût J sans contrainte mais avec un
paramètre λJ
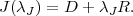 | (3.5) |
Sous une hypothèse de codage indépendant des différentes sous-bandes et
d’additivité pour les mesures de distorsion et de débit, on montre que l’optimal
global est atteint lorsque toutes les sous-bandes sont à un même point de
fonctionnement λJ pour leur courbe débit-distorsion. Le problème devient
alors :
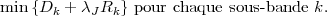 | (3.6) |
La preuve de l’équivalence entre le problème sous contrainte et le problème
sans contrainte est simple et peut être trouvée dans [Sho88].
3.2.2.2 Algorithme
Le débit Rkq pour chaque sous-bande est évalué en utilisant le codeur
arithmétique défini dans [Mof98]. Le choix du codeur n’est pas critique ici. Ce
sont les positions relatives des différents choix possibles qui sont importants, pas
leur performances absolues. Des simulations avec d’autres mesures de débits
comme l’entropie des coefficients des sous-bandes ou par une combinaison de run
length coding et de codage de Rice conduisent à des résultats similaires. Le fait
que les sous-bandes sont codées de manière indépendante est une supposition
implicite ici.
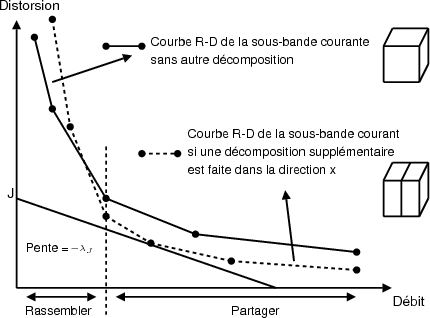
La courbe débit-distorsion est calculée pour les 3 décompositions suivantes
possibles (correspondant aux 3 directions). Une représentation illustrée sur la
figure 3.8 est obtenue. Pour chaque valeur de λJ, la fonction de coût J est
calculée pour chacun des points de la courbe débit-distorsion. La décision
de poursuivre ou non la décomposition est prise selon le coût le plus
faible.
La recherche de type bottom-up est basée sur une fonction récursive et sur la
propriété d’additivité de la fonction de coût J. On note  i,j,kp,q,r la base
optimale de Wi,j,kp,q,r. Soit
i,j,kp,q,r la base
optimale de Wi,j,kp,q,r. Soit  i,j,kp,q,r la base de Wi,j,kp,q,r sans aucune
transformation. On a alors une fonction de coût pour une base de représentation,
J(λJ,
i,j,kp,q,r la base de Wi,j,kp,q,r sans aucune
transformation. On a alors une fonction de coût pour une base de représentation,
J(λJ, ) = min{D + λJR} : R et D étant les points de fonctionnement de la
sous-bande représentée sur la base
) = min{D + λJR} : R et D étant les points de fonctionnement de la
sous-bande représentée sur la base  .
.
J est une fonction de coût additive : pour deux bases orthogonales  1 et
1 et  2,
on a
2,
on a
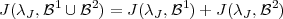 | (3.7) |
en utilisant les propriétés d’additivité des débits et des distorsions.
Proposition 1 (Cas 1D : Coifman, Wickerhauser). Si J est une fonction additive
de coût alors
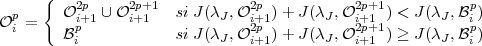 | (3.8) |
Preuve: La meilleure base  ip est soit égale à
ip est soit égale à  ip ou à l’union
ip ou à l’union  0 ∪
0 ∪ 1
des bases de Wi+12p et Wi+12p+1 respectivement. Dans ce dernier cas, la
propriété d’additivité (Eq. 3.7) implique que le coût sur
1
des bases de Wi+12p et Wi+12p+1 respectivement. Dans ce dernier cas, la
propriété d’additivité (Eq. 3.7) implique que le coût sur  ip est minimum si
ip est minimum si  0
et
0
et  1 minimisent le coût sur Wi+12p et Wi+12p+1. On a donc
1 minimisent le coût sur Wi+12p et Wi+12p+1. On a donc  0 =
0 =  i+12p et
i+12p et
 1 =
1 =  i+12p+1. Cela montre que
i+12p+1. Cela montre que  ip est soit
ip est soit  ip, soit
ip, soit  i+12p ∪
i+12p ∪ i+12p+1. La
meilleure base est choisie en comparant le coût des deux possibilités.
__
i+12p+1. La
meilleure base est choisie en comparant le coût des deux possibilités.
__
Ce théorème, formulé à une dimension, peut être étendu au cas à 3
dimensions. A chaque étape on a alors 4 possibilités pour la meilleure
base :
Proposition 2 (Extension à 3 dimensions). Si J est une fonction additive de
coût alors
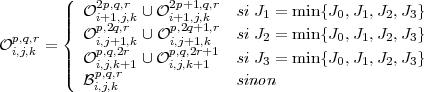 | (3.9) |
En notant
En pratique, l’algorithme est développé de manière récursive. On note J0 le
coût de la sous-bande courante sans réaliser de décomposition supplémentaire.
Les coûts J1, J2 et J3 sont les coûts correspondant à une poursuite de la
décomposition de la sous-bande courante respectivement selon les directions x, y
ou λ. Les coûts J1, J2 et J3 sont calculés par un appel récursif à la fonction de
calcul.
Algorithme 1. Recherche de la décomposition optimale
Fonction récursive : cost(Wi,j,kp,q,r,λJ)
- calcul du coût J0 = J(λJ,
 i,j,kp,q,r) par l’algorithme de Shoham et
Gersho
i,j,kp,q,r) par l’algorithme de Shoham et
Gersho
- calcul du coût J1
- si la taille minimum n’est pas atteinte
selon x : J1 = cost(Wi+1,j,k2p,q,r,λJ) + cost(Wi+1,j,k2p+1,q,r,λJ) par
appels récursifs.
- sinon J1 = ∞
- calcul du coût J2 : similaire à J1
- calcul du coût J3 : similaire à J1
- retourne la valeur min{J0,J1,J2,J3}
Fonction globale
- Pour chaque λJ : appel de cost(W0,0,00,0,0,λJ)
- Courbe R-D complète pour l’image
Cet algorithme conduit à une décomposition optimale différente pour
chaque image et pour chaque débit visé. Il est à noter que grâce à
l’utilisation de la récursivité dans l’algorithme, les points de fonctionnement
seront d’abord calculés pour les sous-bandes les plus petites et ensuite
l’algorithme rassemblera ces valeurs pour prendre la décision de partager ou non
la sous-bande. Cette recherche est exhaustive et ne conduit en aucun cas à un
minimum local.
Cette recherche est similaire dans l’idée à ce qui est fait par Ramchandran
dans [Ram93] avec une extension à un espace 3D anisotropique.
3.2.3 Résultats sur les images 2D
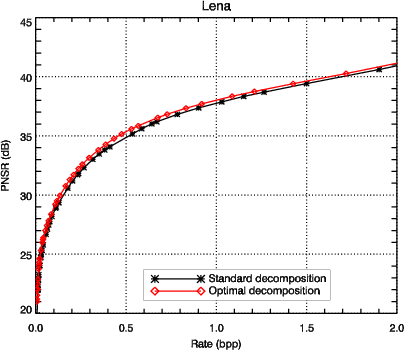
Pour illustration, la recherche de la décomposition optimale est d’abord
appliquée à des images 2D classiques. Le débit est ici estimé avec un codeur
arithmétique. Pour la plupart des images (comme Lena, Fig. 3.9), le gain
apporté par la décomposition optimale ne justifie pas l’augmentation de
complexité. Ce résultat est en accord avec le fait que la décomposition
multirésolution est largement utilisée dans les standards de compression tel que
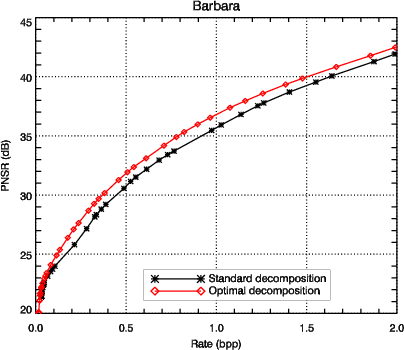
JPEG 2000. Cependant, lorsque l’image a un contenu fréquentiel plus
marqué (comme Barbara, Fig. 3.10), la décomposition optimale arrive à
grouper les coefficients de forte amplitude dans une sous-bande (Fig. 3.10
sous-bande 1) tandis qu’une sous-bande de taille importante (Fig. 3.10
sous-bande 2) arrive à regrouper un grand nombre de coefficients de faible
amplitude. Dans ce cas, le gain peut atteindre 1.5 dB par rapport à la
décomposition multirésolution (pour des débits compris entre 0.2 et 2.0
bpp).
3.2.4 Décomposition en ondelettes optimale pour l’hyperspectral
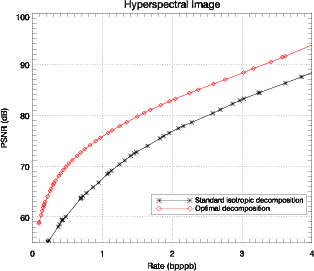
Les résultats présentés sur la figure 3.11 montrent que la décomposition
anisotropique optimale amène une amélioration claire en terme de débit-distorsion.
Ces résultats sont confirmés sur diverses images hyperspectrales. L’amélioration
est d’environ 8 dB en terme de PSNR par rapport à une décomposition
isotropique classique, pour des débits compris entre 0.1 et 4.0 bits par pixel par
bande (bpppb). Si la comparaison est faite en terme de contrainte de qualité, par
exemple pour un PSNR supérieur à 70 dB, le débit nécessaire passe de 1 bpppb
à 0.5 bpppb, soit une réduction d’un facteur 2. L’importance de cette
amélioration par rapport aux images classiques est due à la nature anisotropique
des images hyperspectrales.
3.2.5 Décomposition fixe
Il y a deux inconvénients principaux à cette décomposition optimale :
- Le coût calculatoire de la recherche de la décomposition ;
- La dépendance par rapport à l’image et au débit.
Le coût calculatoire de la méthode est important. Par exemple, la recherche
de la décomposition optimale sur un cube hyperspectral de dimension
256 × 256 × 224 avec une taille minimale de sous-bande de 8 × 8 × 7 (un
maximum de 5 niveaux de décomposition) nécessite de calculer la courbe
débit-distorsion totale pour 250047 sous-bandes. Cette valeur est obtenue en
calculant les combinaisons de toutes les tailles de sous-bandes possibles dans les
trois directions : pour une direction, on a 20 + 21 + … + 25 = 63 tailles possibles,
en combinant dans les 3 dimensions, on a 633 = 250047 sous-bandes
possibles.
La dépendance de la décomposition par rapport à l’image et au débit pose
des problèmes en terme d’implémentation de la transformation. En général, on
préfère des transformations indépendantes des données.
Le but est donc de trouver une décomposition suffisamment proche de la
décomposition optimale pour donner des performances quasi-optimales, tout en
conservant une forme assez générale qui lui permette de rester valable pour
une grande variété d’images. La structure de la décomposition optimale
pour différentes images à différents débits, ainsi que la localisation de la
corrélation résiduelle pour la décomposition isotropique conduit à essayer une
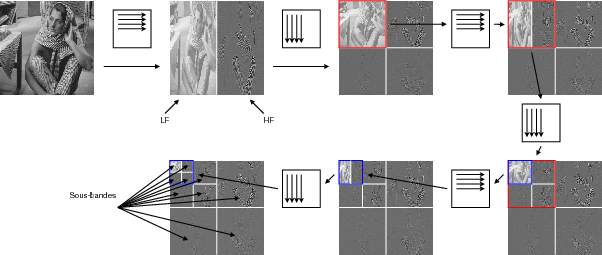
décomposition particulière. Cette décomposition régulière consiste à appliquer
une décomposition multirésolution standard sur les spectres suivie d’une
décomposition multirésolution 2D sur les images résultantes (l’ordre des
opérations étant réversible). Cette décomposition a montré de bonnes
performances dans plusieurs travaux [Kim00,Wan04a], mais uniquement avec une
justification empirique. Une justification théorique en terme d’entropie apparait
dans [Pen06].
La décomposition obtenue est présentée sur la figure 3.13. Cette
décomposition est comparée avec la décomposition isotropique classique, les
coefficients en gris représentent les valeurs proches de 0, les coefficients en
blanc sont les coefficients positifs tandis qu’en noir sont les coefficients
négatifs. Comme on peut le voir sur la figure 3.14, cette décomposition
fixe est presque aussi performante que la décomposition optimale. La
régularité de cette structure ainsi que les faibles perspectives de gain
possibles à chercher une autre décomposition conduisent à choisir cette
décomposition.
| Fig. 3.13: | Décomposition isotropique classique (a) et décomposition
anisotropique (b) avec 3 niveaux de décomposition (les simulations sont
faites avec 5 niveaux). Pour la décomposition isotropique, on peut remarquer
qu’il reste une corrélation importante entre les coefficients dans les basses
fréquences spectrales et spatiales (lignes de coefficients consécutifs de valeur
similaire). Cette corrélation résiduelle est plus faible pour la décomposition
anisotropique. |
|
3.3 Structures d’arbres
3.3.1 Idées principales
Une des faiblesses possibles de JPEG 2000 est qu’il n’utilise pas les relations
existantes entre les localisations des coefficients significatifs entre les différentes
sous-bandes. D’après Taubman [Tau02], le bénéfice venant du choix du point de
troncature compense le fait que les relations entre les coefficients ne sont pas
utilisées. Cette conclusion peut être différente dans le cas des images
hyperspectrales, la corrélation entre les sous-bandes étant anormalement
élevée.
Les arbres de zéros sur les coefficients d’ondelettes ont été développés pour
utiliser la relation qui existe entre la position des singularités dans les différentes
sous-bandes. Après la transformée en ondelettes, on observe que la localisation
des coefficients significatifs est similaire entre les différentes sous-bandes même si
leurs amplitudes sont décorrélées (Fig. 3.15). La propriété à l’origine des arbres
de zéros est que si un coefficient n’est pas significatif dans une
sous-bande alors le coefficient à la même position dans une
sous-bande de plus haute fréquence sera lui aussi probablement non
significatif.
Cette idée a été exploitée avec succès par Shapiro avec EZW (Embedded
Zerotree of Wavelet coefficients) [Sha93]. Une amélioration remarquable a été
apportée quelques années plus tard par Said et Pearlman avec SPIHT (Set
Partitioning In Hierarchical Trees) [Sai96]. Toutefois, les performances des arbres
de zéros sont supérieures à ce qu’on pouvait en attendre [Mar01] et ce succès
n’est pas complètement expliqué. L’idée de SPIHT a ensuite été reprise pour
donner des solutions progressives en résolution [Dan03], résistantes aux
erreurs de transmission [Cho05a] ou généralisées pour des structures 3D,
principalement pour la compression vidéo [Kim00,He03] ou pour les
images médicales [Bil00,Xio03]. Sur le modèle de SPIHT, d’autres codeurs
ont ensuite vu le jour comme SPECK [Isl99,Pea04] qui tire parti des
similarités entre les coefficients adjacents dans une même sous-bande (blocs
de zéros plutôt que des arbres de zéros). SPECK a ensuite été adapté
en SBHP [Chr00] pour concurrencer EBCOT [Tau00] dans la norme
JPEG 2000 ainsi qu’en EZBC [Hsi01] utilisant un codage arithmétique
contextuel évolué pour augmenter les performances. LTW [Oli03], amélioré
dans [Guo06] propose une approche différente pour réduire la complexité. Plus
récemment, SPECK a été adapté pour fournir un codage progressif en
résolution [Xie05].
3.3.2 Principes généraux de EZW et SPIHT
Au moment de sa publication, l’algorithme EZW de Shapiro, utilisant les arbres
de zéros, produisait les meilleures performances en terme de débit-distorsion tout
en ayant une complexité faible. Cette structure d’arbres de zéros a été
généralisée quelques années après par Said et Pearlman pour donner l’algorithme
SPIHT.
Ces deux algorithmes possèdent des propriétés qui les rendent particulièrement
attractifs dans le domaine de la compression spatiale embarquée. Ils produisent
tous deux un train binaire emboîté : le préfixe d’un train binaire produit
par EZW (ou SPIHT) est lui-même un train binaire EZW (ou SPIHT)
valide conduisant à une image décompressée avec une qualité plus faible.
Ces deux algorithmes atteignent ce résultat avec un niveau modeste de
complexité.
La question de la complexité algorithmique est un point critique pour la
définition des algorithmes embarqués, la puissance de calcul étant très limitée.
Cela est particulièrement vrai dans le cas des satellites. Le fait d’avoir un train
binaire emboîté est intéressant pour éviter les dépassements des mémoires et
garantir la meilleure qualité d’image étant données les ressources disponibles à
bord (mémoire et calcul).
Pour assurer cette propriété de train binaire emboîté, la compression
procède par plans de bits. On note cx,y,λ le coefficient de la transformée en
ondelettes de la colonne x, de la ligne y et du plan spectral λ. On définit la suite
de seuils TK-1,…,T0, tels que Tk = Tk+1∕2. Le seuil initial est choisi pour que
|cx,y,λ| < 2TK-1 pour tous les coefficients d’ondelettes. Pour des raisons pratiques
de représentation binaire, on choisit TK-1 comme une puissance de 2. Le
coefficient cx,y,λ est significatif au plan de bits k si |cx,y,λ|≥ Tk. Les plans de bits
sont codés les uns après les autres permettant de réduire la distorsion à chaque
étape.
Un exemple de codage par plan de bits est présenté dans le tableau 3.2. On
considère des coefficients d’ondelettes de valeurs 7, 30 et 180. 7 n’est pas
significatif avant le plan de bits 2, 30 avant le 4 et 180 le devient dès le plan
de bits 7. Après qu’un coefficient ait été marqué comme significatif,
les bits suivants doivent être codés. Le signe des coefficients est codé
séparément.
Pour chaque plan de bits, le codage suit une structure d’arbres de zéros, les
arbres étant définis le long des différentes sous-bandes de la transformée en
ondelettes.
|
|
|
|
| | Plan de bits | Tk | 7 | 30 | 180 |
|
|
|
|
| | 7 | 128 | 0 | 0 | 1 |
| 6 | 64 | 0 | 0 | 0 |
| 5 | 32 | 0 | 0 | 1 |
| 4 | 16 | 0 | 1 | 1 |
| 3 | 8 | 0 | 1 | 0 |
| 2 | 4 | 1 | 1 | 1 |
| 1 | 2 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 |
|
|
|
|
| | |
| Tab. 3.2: | Exemple de codage en plan de bits. |
|
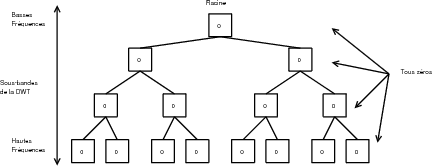
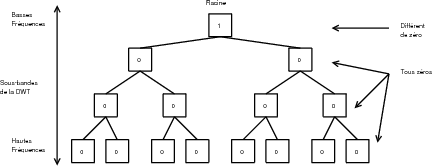
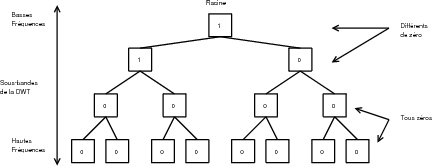
La définition d’un arbre de zéros varie en fonction des algorithmes.
Dans [Cho05b] est développée l’idée des arbres de zéros de degré k. Un arbre de
degré 0 est un arbre dont tous les coefficients sont égaux à zéros (Fig. 3.16), un
arbre de degré 1 est un arbre dont tous les coefficients sauf la racine sont égaux à
zéros (Fig. 3.17) et un arbre de degré 2 est un arbre dont tous les coefficients
sauf la racine et ses enfants directs sont égaux à zéros (Fig. 3.18). EZW utilise
des arbres de degré 0 tandis que SPIHT utilise des arbres de degré 1 et
2.
Un exemple de la première passe des algorithmes EZW et SPIHT est détaillé
dans l’annexe B.
3.3.3 Étude statistique pour le choix de la structure d’arbre
Étant donné la décomposition optimale précédente, plusieurs structures d’arbre
peuvent être définies. On peut utiliser le lien entre les sous-bandes spatiales,
entre les sous-bandes spectrales ou les deux. L’avantage principal des arbres de
zéros est leur capacité de coder un grand nombre de coefficients à zéro (pour le
plan de bits courant) en n’utilisant que très peu de symboles. La structure
d’arbre optimale est donc celle qui maximise la longueur des
arbres de zéros tout en ne laissant qu’un nombre très faible
de zéros isolés. Quelle que soit la structure choisie, les coefficients
significatifs seront les mêmes. La différence dans l’efficacité des structures
d’arbres est uniquement due à leur capacité à rassembler les coefficients
nuls.
Il y a trois structures régulières d’arbre possibles :
- Utiliser uniquement la relation spatiale entre les coefficients : arbres
spatiaux ;
- Utiliser uniquement la relation spectrale entre les coefficients : arbres
spectraux ;
- Utiliser les deux relations : arbres 3D.
Le choix optimal n’est pas évident : mettre plus de coefficients dans un arbre
permet d’encoder potentiellement plus de zéros avec un seul symbole, mais
augmente également le risque d’avoir un coefficient significatif détruisant l’arbre.
Des choix ont été fait précédemment mais sans justifications comme
dans [He03].
Des statistiques sont calculées pour la transformée d’une image
hyperspectrale avec 5 niveaux de décomposition et sont présentées dans les
tableaux 3.3, 3.4 et 3.5. Ces tableaux donnent le nombre de coefficients
significatifs pour chaque plan de bits (qui doivent être codés de toute façon et
sont indépendants de la structure choisie), le nombre de zéros isolés
(IZ) ainsi que le nombre d’arbres de zéros (ZTR). On considère ici les
arbres de degré 0. Pour un plan de bits donné k, tous les coefficients en
dessous du seuil Tk sont à zéro. Le but du codage par arbre de zéros est
d’inclure le maximum de coefficients dans un arbre de 0 en utilisant un
seul symbole (ZTR dans la terminologie EZW comme on le verra plus
tard). Les coefficients en dessous du seuil ne pouvant pas être inclus dans
un arbre de zéros sont codés avec un symbole (IZ). Les deux symboles,
ZTR et IZ, sont utilisés pour coder les coefficients à zéros. Le but de la
structure d’arbre est de minimiser le nombre de symboles utilisés ou de
maximiser le nombre de 0 codés avec un seul symbole. Pour comparer
l’efficacité des différentes structures, le nombre moyen de 0 codés par un
symbole (ZTR ou IZ) est donné ci-dessous dans les trois tableaux 3.3, 3.4,
3.5.
Dans ces tableaux le terme moyenne désigne le nombre de 0 codés
en moyenne par un des symboles IZ ou ZTR. Cette valeur est obtenue
par :
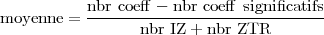 | (3.10) |
Par exemple, pour une structure d’arbre 3D (tab. 3.3), pour le plan de bits
16, 610 symboles sont significatifs, les autres ((256*256*224)-610=14679454) sont
codés par 94+1960 = 2054 symboles, ce qui donne une moyenne de 7146.76
zéros codés par symbole. Cette valeur est à comparer avec l’arbre spatial
pour lequel 15745 symboles sont nécessaires (932.32 zéros codés par
symbole).
|
|
|
|
| | Plan de bits | Significatif | IZ | ZTR | Moyenne |
|
|
|
|
| | 19 | 99 | 0 | 745 | 19704.65 |
| 18 | 183 | 0 | 997 | 14724.05 |
| 17 | 249 | 2 | 1195 | 12263.84 |
| 16 | 610 | 94 | 1960 | 7146.76 |
| 15 | 1143 | 264 | 3595 | 3803.81 |
| 14 | 2975 | 975 | 9619 | 1385.41 |
| 13 | 9052 | 2678 | 28191 | 475.27 |
| 12 | 25525 | 6797 | 66564 | 199.76 |
| 11 | 64646 | 14587 | 122718 | 106.44 |
| 10 | 141869 | 29824 | 189039 | 66.43 |
| 9 | 276589 | 56712 | 268876 | 44.24 |
| 8 | 499196 | 104615 | 372197 | 29.74 |
| 7 | 860482 | 189221 | 517928 | 19.54 |
| 6 | 1461127 | 376246 | 718656 | 12.07 |
| 5 | 2439789 | 691967 | 926441 | 7.56 |
| 4 | 3940555 | 1299399 | 1015978 | 4.64 |
| 3 | 6053237 | 2130317 | 1098716 | 2.67 |
| 2 | 8950166 | 2860847 | 800219 | 1.57 |
| 1 | 11795923 | 2079228 | 341052 | 1.19 |
| 0 | 13673387 | 777902 | 156241 | 1.08 |
|
|
|
|
| | |
| Tab. 3.3: | Statistiques pour une structure d’arbre 3D. |
|
|
|
|
|
| | Plan de bits | Significatif | IZ | ZTR | Moyenne |
|
|
|
|
| | 19 | 99 | 0 | 14534 | 1010.04 |
| 18 | 183 | 0 | 14702 | 998.50 |
| 17 | 249 | 2 | 14842 | 988.94 |
| 16 | 610 | 41 | 15704 | 932.32 |
| 15 | 1143 | 294 | 17256 | 836.41 |
| 14 | 2975 | 1877 | 22564 | 600.51 |
| 13 | 9052 | 10995 | 35115 | 318.17 |
| 12 | 25525 | 39488 | 53933 | 156.87 |
| 11 | 64646 | 95909 | 78453 | 83.82 |
| 10 | 141869 | 179019 | 112395 | 49.89 |
| 9 | 276589 | 297178 | 164097 | 31.23 |
| 8 | 499196 | 480696 | 245862 | 19.52 |
| 7 | 860482 | 787705 | 358326 | 12.06 |
| 6 | 1461127 | 1323093 | 473480 | 7.36 |
| 5 | 2439789 | 2019657 | 543211 | 4.78 |
| 4 | 3940555 | 2783606 | 543079 | 3.23 |
| 3 | 6053237 | 3597503 | 583521 | 2.06 |
| 2 | 8950166 | 4056970 | 316510 | 1.31 |
| 1 | 11795923 | 2557907 | 111127 | 1.08 |
| 0 | 13673387 | 918152 | 56742 | 1.03 |
|
|
|
|
| | |
| Tab. 3.4: | Statistiques pour une structure d’arbre spatial. |
|
|
|
|
|
| | Plan de bits | Significatif | IZ | ZTR | Moyenne |
|
|
|
|
| | 19 | 99 | 0 | 458752 | 32.00 |
| 18 | 183 | 0 | 458752 | 32.00 |
| 17 | 249 | 0 | 458755 | 32.00 |
| 16 | 610 | 57 | 459065 | 31.97 |
| 15 | 1143 | 124 | 459261 | 31.95 |
| 14 | 2975 | 566 | 459575 | 31.90 |
| 13 | 9052 | 1251 | 460365 | 31.78 |
| 12 | 25525 | 2659 | 462871 | 31.48 |
| 11 | 64646 | 4930 | 472529 | 30.61 |
| 10 | 141869 | 12290 | 501134 | 28.31 |
| 9 | 276589 | 32602 | 568224 | 23.97 |
| 8 | 499196 | 84838 | 696563 | 18.15 |
| 7 | 860482 | 210635 | 895402 | 12.49 |
| 6 | 1461127 | 511498 | 1145031 | 7.98 |
| 5 | 2439789 | 1016474 | 1336894 | 5.20 |
| 4 | 3940555 | 1751396 | 1346870 | 3.47 |
| 3 | 6053237 | 2510335 | 1216711 | 2.31 |
| 2 | 8950166 | 3104591 | 763072 | 1.48 |
| 1 | 11795923 | 2154989 | 323541 | 1.16 |
| 0 | 13673387 | 804094 | 142971 | 1.06 |
|
|
|
|
| | |
| Tab. 3.5: | Statistiques pour une structure d’arbre spectral. |
|
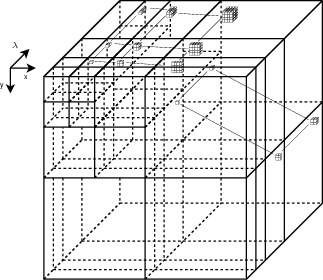
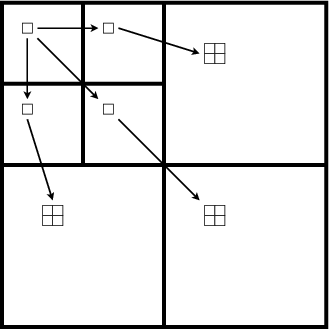
Ces tableaux montrent que le choix de la structure 3D est plus efficace et
utilise moins de symboles pour coder les coefficients à 0 quelque soit le plan de
bits. Cette structure correspond à la structure illustrée sur la figure 3.20. Cette
structure est différente de celle utilisée dans [Tan03] (présentée sur la figure
3.19)
3.3.4 Adaptation de EZW
La partie délicate dans le codage par plan de bits est le codage de la carte des
coefficients significatifs, i.e. l’ensemble des décisions binaires pour savoir si
un coefficient est significatif pour un seuil donné Tk. Les algorithmes
EZW et SPIHT fournissent des moyens efficaces pour coder cet ensemble.
Pour la plupart des coefficients (à l’exception des sous-bandes de plus
basse et de plus haute fréquences), avec la structure d’arbre optimale
précédente, un coefficient cx,y,λ a deux descendants spectraux cx,y,2λ et
cx,y,2λ+1 et quatre descendants spatiaux c2x,2y,λ, c2x+1,2y,λ, c2x,2y+1,λ et
c2x+1,2y+1,λ.
Chaque plan de bits est codé en deux passes. La première passe, appelée
significance pass, code la carte des coefficients significatifs pour le plan de bits
courant. La structure d’arbre de zéros permet de réduire le coût pour le codage
de la carte en utilisant les relations entre les sous-bandes. La deuxième passe,
refinement pass, code un bit pour chaque coefficient ayant été déclaré comme
significatif à un autre plan de bits.
Comme il a été montré par Shapiro, il est utile de coder le signe des
coefficients significatifs en même temps que la carte. En pratique 4 symboles
différents sont utilisés : racine d’un arbre de zéros (Zero Tree Root ou ZTR), zéro
isolé (Isolated Zero ou IZ), coefficient positif (POS) ou coefficient négatif (NEG).
Chacun de ces symboles peut être codé en utilisant 2 bits. IZ signifie que le
coefficient courant est en dessous du seuil mais qu’au moins un de ses
descendants est au dessus (ce coefficient ne peut pas être inclus dans un
arbre de zéros). Le symbole ZTR indique que le coefficient courant est en
dessous du seuil et que tous ses descendants sont également en dessous du
seuil (ou alors sont déjà déclarés comme significatifs et seront de toute
façon traités durant la refinement pass). Le parcours des coefficients
est effectué sous-bande par sous-bande (Fig. 3.21 pour le cas 2D) de
telle manière qu’aucun coefficient ne soit vu avant un de ses parents. Au
sein de chaque sous-bande, les coefficients sont parcourus en zigzag. Le
codage est fait par un alphabet à quatre symboles (POS, NEG, ZTR and
IZ).
Algorithme 2. EZW
Pour chaque plan de bits :
- Significant pass : Pour tous les coefficients non significatifs, coder un
symbole ZTR, IZ, POS ou NEG selon le cas. Les coefficients sont
traités dans l’ordre indiqué sur la figure 3.21.
- Refinement pass : écrire un bit pour tous les coefficients ayant été
déclarés comme significatifs (sauf ceux du dernier plan de bits), ce bit
correspond à la valeur du coefficient dans le plan de bits courant.
_
Un exemple de déroulement de l’algorithme EZW est détaillé dans l’annexe
B.
Il est important de noter que les coefficients ayant déjà été notés comme
significatifs seront traités durant la refinement pass et peuvent donc être inclus
sans dommage dans un arbre de zéros. Une attention particulière doit être
portée sur ce point lors de la programmation de l’algorithme. En effet, dans le
cas d’image 3D, un coefficient peut avoir deux parents (un spatial, un spectral),
conduisant à une situation de croisement d’arbres (tree crossing) illustré sur la
figure 3.22. Ce phénomène est propre à la structure d’arbre redondante utilisée
ici.
Les performances sur l’image moffett3 sont détaillées dans le tableau 3.6 pour la
structure d’arbre 3D ainsi que pour la structure plus classique d’arbre spatial. Un
codeur arithmétique peut être appliqué sur le train binaire en sortie du codeur.
Le codeur arithmétique utilisé est décrit dans [Mof98] et disponible dans un but
de recherche à l’adresse http://www.cs.mu.oz.au/~alistair/arith_coder/.
Le codeur arithmétique (pour les résultats noté AC) est appliqué directement
sur le train EZW et ne prend en compte aucun contexte. Comme on peut le voir
dans le tableau 3.6, la structure d’arbre 3D amène une amélioration significative
par rapport à l’arbre spatial.
|
|
| | | 1.0 bpppb | 0.5 bpppb |
|
|
| | EZW-3D | 73.77 dB | 67.98 dB |
| EZW-3D-AC | 75.54 dB | 69.25 dB |
|
|
| | EZW-spat | 71.94 dB | 66.31 dB |
| EZW-spat-AC | 74.87 dB | 68.84 dB |
|
|
| | |
| Tab. 3.6: | Performances de EZW sur moffett3 (PSNR). 3D correspond à
l’utilisation de la structure d’arbre 3D, spat à l’utilisation de la structure
d’arbre spatial, AC signale l’utilisation d’un codeur arithmétique. La
structure d’arbre 3D amène une amélioration significative. |
|
3.3.5 Adaptation de SPIHT
L’algorithme SPIHT est présenté par Said et Pearlman dans [Sai96]. Les
principales propriétés de EZW sont préservées : codage progressif et faible
complexité. Cependant, quelques différences conduisent à une amélioration pour
les images 2D classiques. L’algorithme SPIHT maintient trois listes de
coefficients : la liste des coefficients significatifs (List of Significant Pixels ou LSP),
la liste des coefficients non significatifs (List of Insignificant Pixels ou LIP)
et la liste des ensembles non significatifs (List of Insignificant Sets ou
LIS).  (x,y,λ) est l’ensemble des enfants de (x,y,λ) (un seul niveau
de descendance),
(x,y,λ) est l’ensemble des enfants de (x,y,λ) (un seul niveau
de descendance), 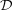 (x,y,λ) est l’ensemble de tous les descendants et
(x,y,λ) est l’ensemble de tous les descendants et
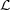 (x,y,λ) =
(x,y,λ) = 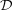 (x,y,λ) -
(x,y,λ) - (x,y,λ) est l’ensemble des descendants à l’exception
des enfants (Fig. 3.23). La fonction St(x,y,λ) est égale à 0 si tous les
descendants de (x,y,λ) sont en dessous du seuil Tt (arbre de zéros) et 1 dans le
cas contraire.
(x,y,λ) est l’ensemble des descendants à l’exception
des enfants (Fig. 3.23). La fonction St(x,y,λ) est égale à 0 si tous les
descendants de (x,y,λ) sont en dessous du seuil Tt (arbre de zéros) et 1 dans le
cas contraire.
La première différence à noter par rapport à EZW est que toute sortie est
binaire. La seconde différence est que l’ordre de traitement des coefficients est
dépendant des données. Alors que les coefficients sont traités en zigzag dans
chaque sous-bande pour EZW (Fig. 3.21), le système de liste de SPIHT laisse
l’ordre entièrement dépendant des données. Les coefficients sont traités selon leur
position dans les listes. Une autre différence à noter est la relation parent-enfant
pour la sous-bande de plus basse fréquence (Fig. 3.24). Dans le cas 2D pour
EZW, chaque coefficient pour la sous-bande basses fréquences (LL) possède
3 descendants (dans LH, HL et HH). Pour SPIHT, un descendant sur
quatre n’a pas de descendant tandis que les autres en ont 4. La définition
des arbres est aussi sensiblement différente car SPIHT considère deux
types d’arbres de zéros : le type A où tous les descendants ne sont pas
significatifs (arbre de degré 1) et le type B où tous les descendants, à
l’exception d’au moins un des enfants, ne sont pas significatifs (arbre
de degré 2). Il est à noter que dans les deux cas, rien n’est dit sur la
valeur du coefficient à la racine qui peut être significatif. Un exemple du
déroulement de SPIHT dans le cas d’images 2D est donné dans l’annexe
B.
Sur les images hyperspectrales avec la relation entre les coefficients définis
précédemment, l’algorithme SPIHT se déroule selon :
Algorithme 3. SPIHT Anisotropique
Initialisation :
- Pour chaque plan de bits t :
- LSP = ∅
- LIP : tous les coefficients sans parent (coefficients de la LLL)
- LIS : tous les coefficients de la LIP qui ont des descendants (marqués comme
type A, par défaut)
Sorting pass :
Pour chaque coefficient (x,y,λ) de la LIP
- Écrire St(x,y,λ)
- Si St(x,y,λ) = 1, déplacer (x,y,λ) dans la LSP et écrire le signe de cx,y,λ
Pour chaque coefficient (x,y,λ) de la LIS
- Si le coefficient est de type A
- Écrire St(
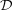 (x,y,λ))
(x,y,λ))
- Si St(
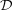 (x,y,λ)) = 1 alors
(x,y,λ)) = 1 alors
- Pour tout (x′,y′,λ′)

 (x,y,λ) : écrire St(x′,y′,λ′) ; si St(x′,y′,λ′) =
1, ajouter (x′,y′,λ′) à la LSP et écrire le signe de cx′,y′,λ′ sinon,
ajouter (x′,y′,λ′) à la fin de la LIP. (Étape critique pour le problème du
tree-crossing).
(x,y,λ) : écrire St(x′,y′,λ′) ; si St(x′,y′,λ′) =
1, ajouter (x′,y′,λ′) à la LSP et écrire le signe de cx′,y′,λ′ sinon,
ajouter (x′,y′,λ′) à la fin de la LIP. (Étape critique pour le problème du
tree-crossing).
- Si
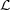 (x,y,λ)
(x,y,λ)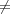 ∅, déplacer (x,y,λ) à la fin de la LIS comme une entrée
de type B
∅, déplacer (x,y,λ) à la fin de la LIS comme une entrée
de type B
- Sinon, retirer (x,y,λ) de la LIS
- Si l’entrée est de type B
- Écrire St(
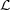 (x,y,λ))
(x,y,λ))
- Si St(
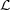 (x,y,λ)) = 1
(x,y,λ)) = 1
- Ajouter tous les (x′,y′,λ′)

 (x,y,λ) à la fin de la LIS comme entrée
de type A
(x,y,λ) à la fin de la LIS comme entrée
de type A
- Retirer (x,y,λ) de la LIS
Refinement pass :
- Pour tous les coefficients (x,y,λ) de la LSP à l’exception de ceux ajoutés au
cours de la dernière sorting pass : Écrire le teme bit le plus significatif de cx,y,λ
Décrémenter t et retourner à la sorting pass. __
Le décodeur est obtenu en remplaçant écrire par lire dans l’algorithme
précédent.
Le phénomène de tree-crossing a un impact plus grand dans le cas de SPIHT
que dans le cas de EZW. Durant l’algorithme, un coefficient peut être traité
avant qu’un de ses parents ne le soit, un soin particulier doit être pris pour éviter
de traiter le même coefficient plusieurs fois. On garde donc en mémoire le fait
qu’un coefficient a déjà été traité. Cette information n’a pas besoin d’apparaître
dans le train binaire de sortie, le décodeur partageant les états du codeur, il sera
capable de faire la même opération. Le phénomène du tree-crossing a
un impact plus important probablement parce que la destruction d’un
arbre (par apparition d’un coefficient significatif) a des conséquences
plus importantes pour SPIHT, qui essaie de maintenir des arbres au
maximum (par le biais des arbres de degrés 1 et 2), que pour EZW. Grâce
aux arbres de degrés 1 et 2, SPIHT tire également plus parti du lien
spectral apparaissant uniquement pour les coefficients de basse fréquence
spatiale.
Le codeur arithmétique utilisé pour EZW (voir paragraphe précédent) peut
être intégré en sortie de cette extension de SPIHT.
D’après le tableau 3.7, on peut remarquer que la structure d’arbre 3D donne
des résultats plus faibles que ce qu’on attendait et n’apporte pas d’amélioration
par rapport à l’arbre spatial. Ces résultats surprenants sont dus au problème du
tree-crossing qui est plus problématique dans le cas de SPIHT (on ne contrôle
pas l’ordre de traitement des coefficients). Sur la figure 3.25 sont présentées les
performances de SPIHT en utilisant la structure d’arbres 3D tandis que
sur la figure 3.26, SPIHT2 correspond au codeur utilisant la structure
d’arbre spatial. Tous des résultats sont commentés dans le paragraphe
suivant.
|
|
| | | 1.0 bpppb | 0.5 bpppb |
|
|
| | SPIHT-3D | 73.55 dB | 68.35 dB |
| SPIHT-3D-AC | 73.89 dB | 68.83 dB |
|
|
| | SPIHT-spat | 75.74 dB | 69.97 dB |
| SPIHT-spat-AC | 75.92 dB | 70.05 dB |
|
|
| | |
| Tab. 3.7: | Performances de SPIHT sur moffett3 en PSNR. 3D correspond
à l’utilisation de la structure d’arbre 3D, spat à l’utilisation de la structure
d’arbre spatial, AC signale l’utilisation d’un codeur arithmétique. Le
phénomène de tree-crossing cause plus de problèmes que dans le cas de
EZW, la structure d’arbre 3D ne donne pas de bons résultats dans ce cas. |
|
3.4 Comparaison des résultats
JPEG 2000, ainsi que les adaptations de EZW et SPIHT sont appliqués sur les
données hyperspectrales du capteur AVIRIS du JPL/NASA ainsi que sur le
capteur spatial Hyperion de la NASA (en conservant toutes les bandes
spectrales pour AVIRIS et en enlevant les bandes noires pour Hyperion :
224 bandes dans les deux cas). Les images sélectionnées sont présentées
sur la figure 3.12. Une des scènes est également utilisée dans d’autres
publications [Tan03].
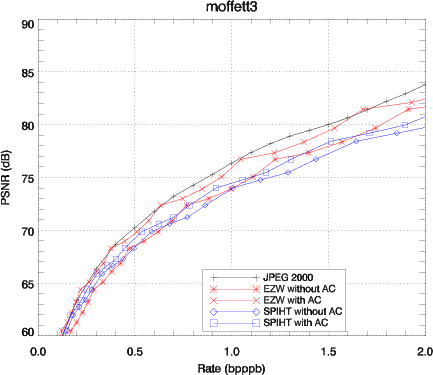
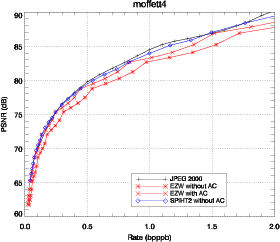
La comparaison entre l’adaptation de JPEG 2000 (présenté dans la
partie 3.1.2) et l’adaptation faite dans [Ruc05] ont des performances
similaires. Les adaptations de EZW et de SPIHT sont comparées avec JPEG
2000. EZW est utilisé avec la structure d’arbre 3D. SPIHT est d’abord
comparé avec la structure d’arbre 3D (Fig. 3.25) puis est utilisé avec la
structure d’arbre spatial (Fig. 3.26). Les résultats obtenus avec JPEG 2000
consistent en une étape de compression en utilisant plusieurs niveaux de
qualité (quality layers) [ISO02]. 20 niveaux de qualité sont définis de
0.1 bpppb à 2.0 bpppb. La décompression est faite aux niveaux de qualité
correspondants. Les performances de EZW et SPIHT sont calculées avec
et sans codeur arithmétique. Les performances sont tracées en terme
de PSNR (Eq. 2.11). L’image est complètement compressée, le train
binaire sauvegardé sur disque puis décodé. Le PSNR est mesuré entre
l’image originale et l’image en sortie (pas sur la distorsion de l’image
transformée).
Les performances de EZW-3D sont bien meilleures lorsque la décompression
atteint la fin d’un plan de bits. Les pics de performance correspondent aux points
d’inflexion sur la figure 3.25. Cette caractéristique n’apparaît pas pour SPIHT.
Utilisé avec un codeur arithmétique, EZW-3D produit des performances
similaires à JPEG 2000 et même meilleures à certains débits. Les performances
de SPIHT-3D sont étonnamment mauvaises pour des forts débits et tendent à
dépasser EZW-3D pour des débits plus faibles. Cela peut être expliqué par le fait
que SPIHT utilisé avec une structure d’arbre 3D est particulièrement sensible au
tree-crossing.
La solution la plus simple pour éviter le tree-crossing est d’utiliser la
structure d’arbre spatial définie auparavant. Cette modification conduit à une
structure similaire à celle trouvée dans [He03] et apporte une amélioration,
comme on peut le voir sur la figure 3.26 (SPIHT-spat). Dans le cas de SPIHT, le
codeur arithmétique apporte une amélioration faible. Les résultats sont donc
présentés sans codeur arithmétique ce qui présente en plus l’avantage de
réduire la complexité du codeur. Cette solution n’est pas entièrement
satisfaisante car on peut voir que la relation spectrale entre les pixels n’est pas
complètement utilisée. Cependant, conserver la structure 3D et tirer parti
du tree-crossing demanderait de grandes modifications sur l’algorithme
SPIHT.
3.5 Variations avec la notation binaire signée
3.5.1 Un inconvénient de EZW
Un des défauts de EZW est la mémoire requise pour mémoriser les coefficients
qui ont été notés comme significatifs. Ces coefficients seront traités pendant la
refinement pass, il n’est donc pas nécessaire de les traiter pendant la significance
pass. Au moins un bit de mémoire est nécessaire pour chaque coefficient de
l’image. Pour une image hyperspectrale de 256 × 256 × 224, en comptant un bit
de mémoire pour signaler la position des coefficients significatifs, on aura
besoin de garder 14.7 Mbits en mémoire durant la compression. Si la
compression est faite plan de bits par plan de bits (en gardant uniquement le
plan de bits courant en mémoire), conserver cette information double la
mémoire nécessaire. Une solution pour éliminer ce besoin de mémoire
est de supprimer la refinement pass. Dans cette situation, on applique
uniquement la significant pass pour chaque plan de bits. Un coefficient
est considéré comme non significatif si le bit de ce coefficient dans ce
plan de bits est 0. Il est considéré comme significatif sinon. Cependant,
ce changement provoque une perte de performances de plus de 2 dB
(Tableau 3.8).
| Débit | 3D-EZW | Sans refinement pass
| | (bpppb) | MSE | PSNR | MSE | PSNR |
|
|
|
|
| | 1.0 | 106.15 | 76.07 | 193.73 | 73.46 |
| 0.5 | 445.22 | 69.84 | 685.49 | 67.97 |
| |
| Tab. 3.8: | Effet de la suppression de la refinement pass. Les résultats sont
pour l’image Moffett3. |
|
3.5.2 Utilisation de la notation binaire signée
Comme nous l’avons vu, les bonnes performances des techniques par arbres de
zéros proviennent principalement de leur capacité à coder une grande quantité de
zéros avec un seul symbole. Si tous les plans de bits sont codés par une
significance pass, la probabilité d’avoir des zéros dans les plans de bits
inférieurs devient proche de 0.5. D’autre part, ces zéros tendent à être
distribués aléatoirement empêchant ainsi les arbres de zéros de les coder
efficacement.
Une stratégie possible pour augmenter les performances des arbres de zéros
est d’augmenter la proportion de zéros dans chaque plan de bits. La notation
binaire signée permet de réaliser cela. La notation binaire signée d’un nombre n
est une suite de chiffres a = (…,a2,a1,a0) avec ai  {-1,0,1} tel que
n = ∑
i=0∞ai2i.
{-1,0,1} tel que
n = ∑
i=0∞ai2i.
Le nombre 119, par exemple, en notation binaire classique est (0,1,1,1,0,1,1,1)
car il est égal à 1 * 26 + 1 * 25 + 1 * 24 + 1 * 22 + 1 * 21 + 1 * 20. Si -1 est utilisé en
plus de 1 et 0, le nombre 119 peut être représenté par (1,0,0,0,-1,0,0,-1) car
il est égal à 1 * 27 - 1 * 23 - 1 * 20.
La représentation binaire signée pour un nombre donné n’est pas
unique. En général, l’intérêt est d’avoir une représentation qui contient un
maximum de 0. Cette représentation est obtenue en considérant la solution de
poids de Hamming minimum. Le poids de Hamming d’une représentation
est égal au nombre de chiffres non nul dans la représentation a. Dans
l’exemple précédent, le poids de Hamming de la représentation de 119 en
notation binaire classique est 6 tandis qu’il est de 3 dans la notation binaire
proposée.
Dans [Arn93] un algorithme est donné pour obtenir la représentation binaire
signée de poids de Hamming minimum :
Algorithme 4.
Représentation binaire signée
t = 0
a = (…,a2,a1,a0), la notation binaire classique du nombre à convertir
Tant que (…,at+2,at+1,at)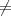 (…,0,0,0)
(…,0,0,0)
- Si at
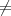 0
0
- b = (…0, sgn(at), -2*sgn(at),0, …,0) (les éléments non nuls à t, t+1)
- c = a + b
- si ct+1 = 0
- t = t + 1
retourner a _
Cet algorithme est simple, mais ce n’est pas le plus efficace en terme de
complexité. Des algorithmes plus rapides existent pour réaliser cette convertion
en nombre binaire signés de poids de Hamming minimum. On peut citer par
exemple [Pro00,Joy00,Oke04].
Cependant la notation binaire signée de poids minimum n’est pas unique. En
général, la notation binaire signée est utilisée pour l’exponentiation rapide. La
forme non-adjacente (NAF), où les éléments différents de zéros sont séparés par
au moins un zéro, est unique et possède les propriétés nécessaires pour
l’exponentiation rapide. La plupart des algorithmes de conversion conduisent à
cette forme.
Dans notre cas, si le poids de Hamming minimum est une condition requise
(le maximum de zéros), il n’est pas sûr que la NAF ait un avantange par rapport
aux autres possibilités. Deux possibilités sont comparées dans la suite en
utilisant la transformation (…,1,0,-1,…) → (…,0,1,1,…) et de même
(…,-1,0,1,…) → (…,0,-1,-1,…). Nous appellerons cette seconde forme AF
(Adjacent Form). Ces deux formes donnent le même nombre de zéros. Des
exemples de représentation binaire signée pour le nombre 349 sont donnés dans
le tableau 3.9.
| t | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 2t | 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|
|
|
|
|
|
|
|
|
|
| | Binaire | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 |
| NAF | 1 | 0 | -1 | 0 | -1 | 0 | 0 | -1 | 0 | 1 |
| AF | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | -1 | -1 |
| |
| Tab. 3.9: | Exemple de représentations pour le nombre 349 |
|
Pour mesurer l’efficacité à accroître la proportion de coefficients à zéros, on
calcule cette proportion après le premier bit significatif. Pour la transformée en
ondelettes de moffett3, le nombre moyen de bits après le premier bit significatif,
le nombre de zéros après ce premier bit significatif et la proportion de bits
à zéro sont détaillés dans le tableau 3.10. La notation binaire signée
permet d’accroître de manière significative la proportion de zéros pour les
plans de bits inférieurs : plus de 60% de zéros contre 50% avant. Ces
résultats confirment ce qui était attendu pour la représentation binaire
signée.
| Notation | Nombre moy. de bits | Nombre de | Proportion de |
| | après le 1er sig. | bits à zéro | bits à zéro |
|
|
|
| | Binaire | 2.72 | 20 490 955 | 51.28% |
| NAF | 3.12 | 29 263 791 | 63.83% |
| AF | 2.85 | 25 507 573 | 61.03% |
| |
| Tab. 3.10: | La proportion de bits à zéros après le premier bit significatif. |
|
EZW est implémenté en utilisant la notation binaire signée (NAF et AF) et
chaque plan de bits est traité en utilisant uniquement la significant pass.
Cependant, même si on observe un gain de 1 dB en utilisant la notation binaire
signée (Tableau 3.11), cette amélioration n’est pas suffisante pour récupérer la
baisse de performances due à la suppression de la refinement pass. On ne retrouve
pas les performances du tableau 3.8. Dans ce cas, on ne constate pas de
différences entre les formes NAF et AF.
| Débit | Binaire | NAF | AF
| | (bpppb) | MSE | PSNR | MSE | PSNR | MSE | PSNR |
|
|
|
|
|
|
| | 1.0 | 193.73 | 73.46 | 149.07 | 74.60 | 151.76 | 74.52 |
| 0.5 | 685.49 | 67.97 | 549.56 | 68.93 | 553.10 | 68.90 |
| |
| Tab. 3.11: | EZW avec traitement séparés de chaque plan de bits (sans
refinement pass). |
|
3.5.3 Utiliser les dépendances spatiales
Cette dernière version du codeur EZW ne prend pas en compte la valeur des
coefficients voisins dans le même plan de bits. Un moyen simple de les prendre en
compte est d’utiliser un codeur arithmétique contextuel. On considère
uniquement trois coefficients dans le même plan de bits : ces coefficients
sont ceux précédant le pixel courant dans les trois directions du cube
hyperspectral.
On considère également la valeur du coefficient à la même place dans le plan
de bits précédent. Dans le cas de la NAF, cette dépendance est facile à prendre
en compte : si un coefficient dans le plan de bits précédent est 1 ou -1, on sait
que le coefficient courant est 0. Dans le cas de la forme AF, cette règle n’existe
pas. On aurait donc à doubler le nombre de contextes selon les cas où le
coefficient dans le plan de bits précédent appartient aux ensembles {0} ou
{-1,1}. On choisit donc la forme NAF pour laquelle le contexte est plus
simple.
Soient ηs, ηl et ηb, les coefficients précédents dans les trois directions :
- ηs(i,j,k) = (i - 1,j,k)
- ηl(i,j,k) = (i,j - 1,k)
- ηb(i,j,k) = (i,j,k - 1)
Comme les plans de bits sont pris en compte séparement, ηs, ηl et ηb font
partie de l’ensemble {-1,0,+1}. On considère la fonction qui, à une combinaison
de voisinage, associe une valeur η définie par η = ηs + 3ηl + 9ηb. Cette fonction
est une bijection entre tous les voisinages possibles et les entiers entre -13 et
13.
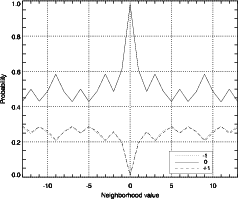
On peut donc étudier la probabilité d’avoir une des valeurs -1, 0 ou 1 selon
les valeurs voisines. La courbe de probabilité est représentée sur la figure 3.27.
Ces probabilités sont calculées pour l’image moffett3 de 256 × 256 × 224 pour
tous les plans de bits pour la forme NAF : plusieurs millions de bits sont donc pris
en compte. On peut voir qu’un voisinage se distingue clairement des
autres en terme de probabilité : quand η = 0 (ηs = ηl = ηb = 0). Avec ce
voisinage, la probabilité d’avoir un 0 pour le coefficient courant est très
élevée.
Le contexte pour le codeur arithmétique est donc séparé en deux cas : η = 0
et η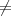 0.
0.
On peut noter également que dans le cas de la NAF, une valeur différente de
0, pour un coefficient dans un plan de bits donné, sera nécessairement suivie par
un coefficient à 0 dans le plan de bits suivant (d’où son nom de non-adjacent
form). Dans ce cas, il n’est pas nécessaire de sortir une information.
Cet avantage n’apparaît pas pour la forme AF qui ne donne pas d’aussi
bonnes performances. Les performances obtenues sont présentées dans le
tableau 3.12
| Débit | Non contextuel | Contextuel
| | (bpppb) | MSE | PSNR | MSE | PSNR |
|
|
|
|
| | 1.0 | 149.07 | 74.60 | 121.38 | 75.49 |
| 0.5 | 549.56 | 68.93 | 457.77 | 69.72 |
| |
| Tab. 3.12: | EZW avec un codage indépendant pour chaque plan de bits en
forme NAF avec et sans codage contextuel. |
|
On nomme cette dernière version de EZW sans refinement pass utilisant une
forme NAF et un codage arithmétique contextuel 3D-EZW-NAF.
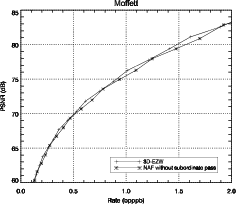
La comparaison entre 3D-EZW-NAF et 3D-EZW est présentée dans le
tableau 3.13 pour l’image moffett3. Les courbes débit-distorsion sont illustrées
sur la figure 3.28.
| Débit | 3D-EZW | 3D-EZW-NAF
| | (bpppb) | MSE | PSNR | MSE | PSNR |
|
|
|
|
| | 1.0 | 106.15 | 76.07 | 121.38 | 75.49 |
| 0.5 | 445.22 | 69.84 | 457.77 | 69.72 |
| 0.25 | 1407.34 | 64.85 | 1514.81 | 64.53 |
| 0.125 | 3933.86 | 60.38 | 4402.34 | 59.89 |
| |
| Tab. 3.13: | Comparaison entre 3D-EZW et 3D-EZW-NAF sur l’image
moffett3. |
|
Les performances de 3D-EZW-NAF sont très proches de celle de 3D-EZW.
En terme de complexité calculatoire, une estimation précise serait requise, mais
un moyen simple d’avoir une première estimation est de comparer les temps
d’exécution. Le temps de codage est similaire entre 3D-EZW et 3D-EZW-NAF :
environ 100 s pour les deux versions. La conversion en notation binaire signée
n’est pas optimisée dans notre cas (ajoutant environ 24 s) mais pourrait être
optimisée en utilisant un algorithme plus performant disponible dans la
littérature. Comme l’une des utilisations majeures de la notation binaire signée
est d’accélérer l’exponentiation rapide, une conversion rapide ne sera pas un
problème.
Il est à noter que l’intérêt principal de cet algorithme est qu’il est facilement
parallélisable sans compromis de rapidité/complexité. On peut imaginer utiliser
différentes unités de codage pour coder chaque plan de bits. Chacune de ces
unité prendra en entrée un plan de bits et sortira la portion du train binaire
correspondant à ce plan de bits.
3.6 Conclusion
Dans ce chapitre, différentes méthodes de compression pour les images
hyperspectrales sont développées puis comparées. En premier lieu, une méthode
est définie pour trouver la décomposition optimale (au sens débit-distorsion) en
ondelettes anisotropiques 3D pour les images hyperspectrales. Cette méthode
justifie l’utilisation d’une décomposition fixée particulière. Sur cette
décomposition, plusieurs structures d’arbre peuvent être définies. Une étude
statistique sur la proportion d’arbre de zéros est faite pour différentes structures
possibles et conduit à un choix de structure d’arbre 3D. Ensuite, différents
algorithmes de compression basés sur cette transformation et cette structure
d’arbre sont définis. La première méthode est une adaptation de l’algorithme
EZW, la seconde une adaptation de SPIHT. Leurs résultats sont comparés au
standard JPEG 2000. Même si l’optimisation débit-distorsion incluse
dans le standard JPEG 2000 rend difficile son implémentation dans le
contexte spatial, ses performances peuvent être vues comme un objectif à
atteindre.
Cette étude monte l’intérêt des arbres de zéros adaptés sur une
décomposition anisotropique pour la compression des images hyperspectrales.
Avec une complexité faible, EZW pour une structure d’arbre 3D présente des
performances très proches de JPEG 2000 tout en produisant un train
binaire emboîté. SPIHT-spat donne de bonnes performances même sans
codeur arithmétique. Ces propriétés sont particulièrement intéressantes
dans le contexte de la compression bord des images hyperspectrales. Des
améliorations sont toujours possibles, particulièrement dans le cas de SPIHT
si on arrive à trouver un moyen de tirer parti de la structure d’arbre
3D.
La notation binaire signée, particulièrement la non-adjacent form, a montré
de bonne capacité à compenser la suppression de la refinement pass. Cette
compensation a permis à un algorithme simplifié de donner des performances
presque aussi bonnes que l’algorithme de départ. Cette utilisation originale de la
notation binaire signée semble prometteuse et pourrait être appliquée à d’autres
algorithmes de compression.
These en pdf
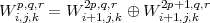
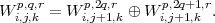
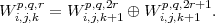
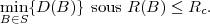
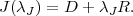
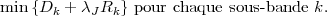
 i,j,kp,q,r la base
optimale de Wi,j,kp,q,r. Soit
i,j,kp,q,r la base
optimale de Wi,j,kp,q,r. Soit  i,j,kp,q,r la base de Wi,j,kp,q,r sans aucune
transformation. On a alors une fonction de coût pour une base de représentation,
J(λJ,
i,j,kp,q,r la base de Wi,j,kp,q,r sans aucune
transformation. On a alors une fonction de coût pour une base de représentation,
J(λJ, ) = min{D + λJR} : R et D étant les points de fonctionnement de la
sous-bande représentée sur la base
) = min{D + λJR} : R et D étant les points de fonctionnement de la
sous-bande représentée sur la base  .
.
 1 et
1 et  2,
on a
2,
on a
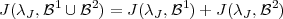
 ip est soit égale à
ip est soit égale à  ip ou à l’union
ip ou à l’union  0 ∪
0 ∪ 1
des bases de Wi+12p et Wi+12p+1 respectivement. Dans ce dernier cas, la
propriété d’additivité (Eq. 3.7) implique que le coût sur
1
des bases de Wi+12p et Wi+12p+1 respectivement. Dans ce dernier cas, la
propriété d’additivité (Eq. 3.7) implique que le coût sur  ip est minimum si
ip est minimum si  0
et
0
et  1 minimisent le coût sur Wi+12p et Wi+12p+1. On a donc
1 minimisent le coût sur Wi+12p et Wi+12p+1. On a donc  0 =
0 =  i+12p et
i+12p et
 1 =
1 =  i+12p+1. Cela montre que
i+12p+1. Cela montre que  ip est soit
ip est soit  ip, soit
ip, soit  i+12p ∪
i+12p ∪ i+12p+1. La
meilleure base est choisie en comparant le coût des deux possibilités.
__
i+12p+1. La
meilleure base est choisie en comparant le coût des deux possibilités.
__


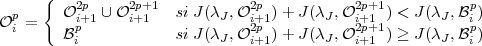
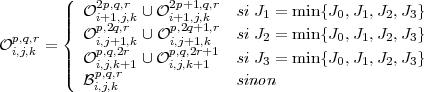
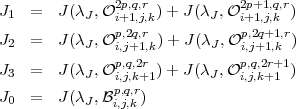




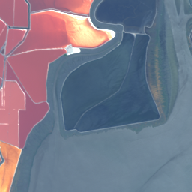 (a) Moffett4
(a) Moffett4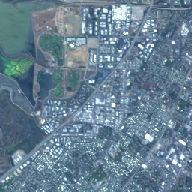 (b) Moffett3
(b) Moffett3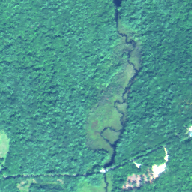 (c) Harvard1
(c) Harvard1 (d) Hawaii1
(d) Hawaii1 (e) Hawaii2
(e) Hawaii2 (f) Hyperion1
(f) Hyperion1 (a)
(a) (b)
(b)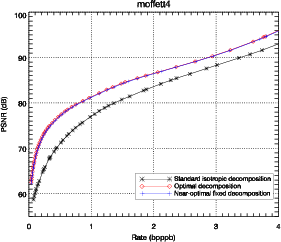 (a) moffett4
(a) moffett4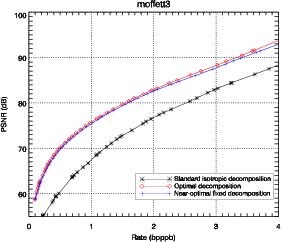 (b) moffett3
(b) moffett3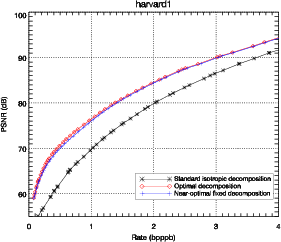 (c) Harvard1
(c) Harvard1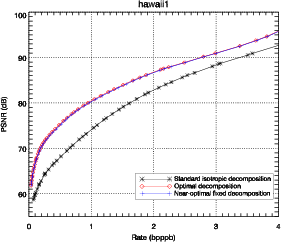 (d) Hawaii1
(d) Hawaii1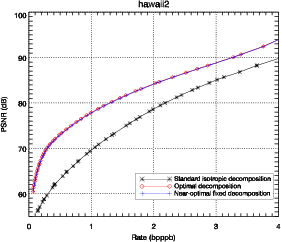 (e) Hawaii2
(e) Hawaii2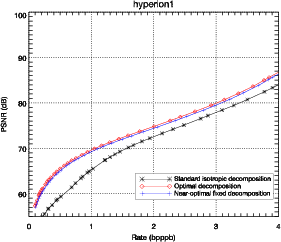 (f) hyperion1
(f) hyperion1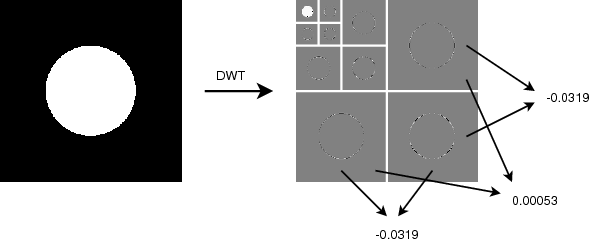
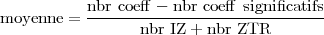
 (a)
(a)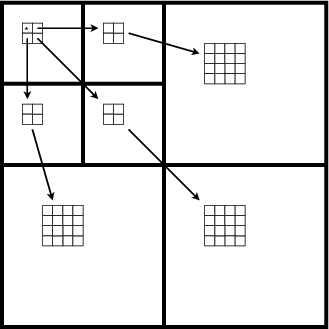 (b)
(b)
 (a) moffett4
(a) moffett4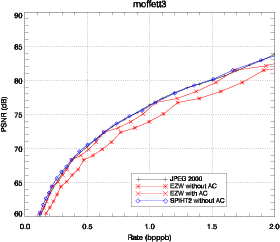 (b) moffett3
(b) moffett3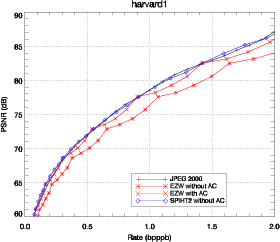 (c) Harvard1
(c) Harvard1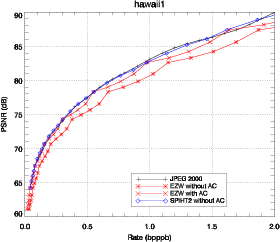 (d) Hawaii1
(d) Hawaii1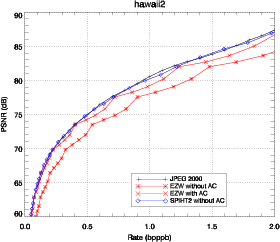 (e) Hawaii2
(e) Hawaii2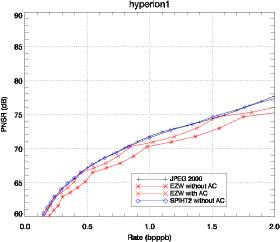 (f) hyperion1
(f) hyperion1