Compression des images hyperspectrales
These en pdf
Annexe A
DWT
IL existe de nombreux tutoriaux concernant la théorie et l’utilisation des ondelettes. Cette annexe n’a pas la prétention de les remplacer, elle regroupe les informations utiles concernant les transformées en ondelettes discrètes (DWT) utilisées dans cette étude pour référence.
A.1 Implémentation générale
Deux approches principales existent pour la transformée en ondelette, la convolution et le lifting scheme. La convolution correspond à la vision traditionnelle du filtrage. Le lifting scheme [Dau98] permet une implémentation plus rapide et surtout les transformées d’entier en entier. On se place ici dans le contexte des ondelettes discrètes biorthogonales.
A.1.1 Approche convolutive
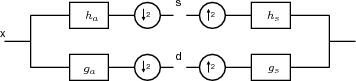
À l’origine, les ondelettes ont été définies sous forme de filtres [Mal89]. L’étape d’analyse correspond à la décomposition en ondelettes du signal et la synthèse à la reconstitution du signal à partir des coefficients d’ondelettes. On note ha le filtre passe-bas d’analyse, ga le filtre passe-haut d’analyse et hs et gs les filtres de synthèse, comme illustré sur la figure A.1.
L’ondelette 9/7 (9 et 7 étant la longueur des filtres passe-bas et passe-haut) est aussi appelée (4,4) (les valeurs correspondant aux nombres de moments nuls des filtres passe-haut et passe-bas). Cette ondelette est quasi-orthogonale et donc particulièrement appréciée dans le cas de la compression avec pertes, c’est d’ailleurs l’ondelette par défaut pour la compression avec pertes de JPEG 2000. Les valeurs numériques des coefficients des filtres sont présentées dans le tableau A.1.
|
L’ondelette 5/3 (5 et 3 étant la longueur des filtres passe-bas et passe-haut) est aussi appelée (2,2) (les valeurs correspondant ici aux nombres de moments nuls des filtres passe-haut et passe-bas). Cette ondelette semble donner de meilleurs performances pour la compression sans pertes, c’est l’ondelette par défaut du standard JPEG 2000 pour la compression réversible. Les valeurs numériques des coefficients des filtres sont présentées dans le tableau A.2.
A.1.2 Approche lifting
Il est montré que la transformée en ondelettes peut se factoriser sous la forme d’étapes de prédiction et d’update [Dau98,Swe97]. La 9/7 peut ainsi se mettre sous cette forme.
En prenant
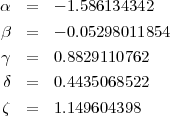
La DWT 9/7 est effectuée par :
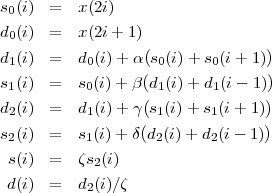
La DWT 5/3 correspond à la suite d’opérations :
Le lifting scheme permet une implémentation moins coûteuse de la transformée en ondelette. Cette approche est particulièrement intéressante au niveau de l’utilisation de la mémoire puisqu’elle permet à la transformée en ondelette d’être réalisé en utilisant uniquement une taille mémoire légèrement supérieure à la taille des données.
A.2 La transformée entière
Un autre point intéressant est la facilité avec laquelle on peut implémenter des transformées d’entier en entier pour permettre la compression sans pertes [Cal98]. On obtient ainsi une transformée en entier correspondant à la DWT 9/7 par :
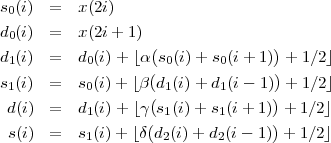
et pour la DWT 5/3 :
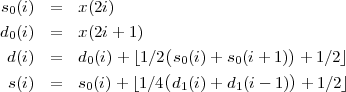
Si on veut conserver une transformée unitaire, il faut ajouter un coefficient d’échelle. Des recherches ont été faites dans [Xio03] pour rendre ce facteur d’échelle compatible avec une transformée sur des entiers.
Dans notre cas, on utilise la transformée d’entier en entier uniquement dans le cas de la compression sans perte, le facteur d’échelle n’a pas d’importance.
A.3 Notation des sous-bandes
Il existe plusieurs notations pour les sous-bandes de la transformée en ondelettes. La figure A.2 présente la notation classique pour la décomposition multirésolution. On reprend cette notation en 3D dans notre cas, principalement pour référence à la sous-bande de plus basse fréquence appelée LLL.
Un exemple de la notation plus générale présentée dans le chapitre 3 appliqué à la décomposition multirésolution est donné sur la figure A.3.